Consider allowing JavaScript. Otherwise, you have to be proficient in
reading ![]() since formulas
will not be rendered. Furthermore, the table of contents in the left
column for navigation will not be available and code-folding not
supported. Sorry for the inconvenience.
since formulas
will not be rendered. Furthermore, the table of contents in the left
column for navigation will not be available and code-folding not
supported. Sorry for the inconvenience.
Examples in this article were generated with
4.4.2 by the packages
survival,1 coin,2
truncnorm,3 reshape,4
lattice,5 and moments.6 An
intermediate knowledge of R is
required. Any version of R would likely be
sufficient to run the examples.
- The right-hand badges give the respective section’s ‘level’.
- Basics about Noncompartmental Analysis (NCA) – requiring no or only limited statistical expertise.
- These sections are the most important ones. They are – hopefully – easily comprehensible even for novices.
- A somewhat higher knowledge of statistics and/or R is required. May be skipped or reserved for a later reading.
- An advanced knowledge of statistics and/or R is required. Not recommended for beginners in particular.
- Click to show / hide R code.
- Click on the icon
in the top left corner to copy R code to the clipboard.
Introduction
What is an ‘apparent’ difference in tmax?
An excellent question! Puzzles me for years…
In early European guidances a nonparametric method was recommeded.
“Statistical evaluation of \(\small{t_\text{max}}\) only makes sense if there is a clinically relevant claim for rapid release or action or signs related to adverse effects. The non-parametric 90 % confidence interval for this measure of relative bioavailability should lie within a clinically determined range.
In the revised guideline the European Medicines Agency abandoned the test and stated for immediate release products:
“A statistical evaluation of \(\small{t_\text{max}}\) is not required. However, if rapid release is claimed to be clinically relevant and of importance for onset of action or is related to adverse events, there should be no apparent difference in median \(\small{t_\text{max}}\) and its variability between test and reference product.
Later the EMA stated for delayed and multiphasic release formulations:
“A formal statistical evaluation of \(\small{t_\text{max}}\) is not required. However, there should be no apparent difference in median \(\small{t_\text{max}}\) and its range between test and reference product.
In recent product-specific guidances for ibuprofen, paracetamol (acetaminophen for American readers), and tadalafil we find:
“Comparable median (≤ 20 % difference) and range for \(\small{T_\text{max}}\).
In a footnote of the guidances find:
“This revision concerns defining what is meant by ‘comparable’ \(\small{T_\text{max}}\) as an additional main pharmacokinetic variable in the bioequivalence assessment section of the guideline.
Terminology
‘Apparent’ is – and for good reasons – not contained in the
statistical toolbox. Not surprising, since according to the guidelines
»a [formal] statistical evaluation of \(\small{t_\text{max}}\) is not
required«.
Now what? Based on gut feeling, reading tea leaves?
These definitions of ‘apparent’ are given in dictionaries:
Macmillan (British English)
- Easy to see or understand.
- An apparent quality, feeling, or situation seems to exist although it may not be real.
Meriam-Webster (American English)
- Open to view, visible.
- Clear or manifest to the understanding.
- Appearing as actual to the eye or mind.
- Manifest to the senses or mind as real or true on the basis of evidence that may or may not be factually valid.
Beauty Lies in the Eye of the Beholder. Paper doesn’t blush…
Hence, the assessment of formulation differences opens the door for interpretation, which is – from a scientific perspective – extremely unsatisfactory.
History & Status
A plot supporting visual inspection was proposed14 but AFAIK, rarely applied (I used it only once in 32 years). An example from my archive:
# sampling time points
smpl <- c(0, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75,
2, 2.25, 2.5, 3, 4, 6, 8, 10, 12)
# subjects’ tmax of R and T
R <- c(1.25, 2.00, 1.00, 1.25, 2.50, 1.25, 1.50, 2.25,
1.00, 1.25, 1.50, 1.25, 2.25, 1.75, 2.50, 2.25)
T <- c(1.50, 0.50, 0.75, 2.25, 0.75, 0.75, 2.25, 2.25,
0.75, 0.75, 1.50, 1.50, 0.75, 1.00, 2.50, 0.50)
n <- max(c(length(R), length(T))) # number of subjects
# vector of observed tmax values (R and T)
obs <- unique(sort(c(R, T)))
# intervals for the pseudo bar charts
int <- smpl[(which(smpl == min(obs))-1):(which(smpl == max(obs))+1)]
# counts
n.R <- n.T <- integer()
for (i in seq_along(int)) {
n.R[i] <- sum(abs(R - int[i]) < 1e-6)
n.T[i] <- sum(abs(T - int[i]) < 1e-6)
}
ylim <- c(-1.04, 1.04) * max(n.R, n.T)
dev.new(width = 4.6, height = 4.6)
op <- par(no.readonly = TRUE)
par(mar = c(4.1, 4, 2, 0), cex.axis = 0.9)
plot(c(0, max(obs) * 1.04), ylim, type = "n", axes = FALSE,
xlab = "Sampling time (h)", ylab = "Number of subjects",
main = expression(italic(t)[max]))
axis(side = 1, at = unique(round(obs, 0)))
axis(side = 1, at = int, labels = FALSE, tcl = -0.25)
axis(side = 2, at = pretty(ylim[1]:ylim[2], 5),
labels = abs(pretty(ylim[1]:ylim[2], 5)), las = 1)
axis(side = 2, at = round((ylim[1]:ylim[2])), labels = FALSE, tcl = -0.25)
abline(h = 0)
mtext("Reference", side = 2, line = 1.75, at = ylim[2] / 2)
mtext("Test", side = 2, line = 1.75, at = ylim[1] / 2)
points(median(R), ylim[2], cex = 1.15, pch = 21, bg = "#BFFFEF", col = "black")
points(median(T), ylim[1], cex = 1.15, pch = 21, bg = "#BFEFFF", col = "black")
legend(median(R), ylim[2], cex = 0.9, box.lty = 0, x.intersp = 0,
yjust = 0.5, legend = bquote(tilde(t)[max] == .(median(R))))
legend(median(T), ylim[1], cex = 0.9, box.lty = 0, x.intersp = 0,
yjust = 0.5, legend = bquote(tilde(t)[max] == .(median(T))))
box()
j <- 1
for (i in seq_along(int)) {
j <- j + 1
D <- (int[i] + int[i+1]) / 2 - int[i]
rect(int[i] + D, 0, int[i+1] + D, n.R[j], col = "#BFFFEF", border = "black")
rect(int[i] + D, 0, int[i+1] + D, -n.T[j], col = "#BFEFFF", border = "black")
}
par(op)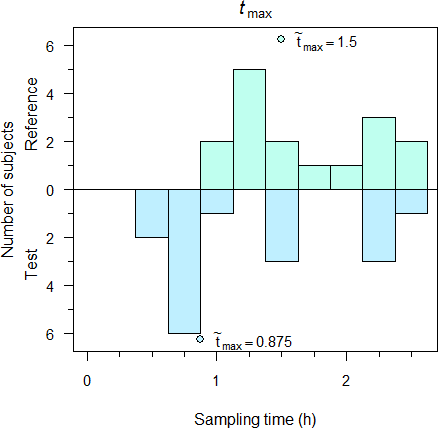
Fig. 1 600 mg IR ibuprofen, single dose fasting, 16 subjects.
Although the plot appears like two bar charts, they aren’t. If sampling intervals are not equally spaced like in this case, the areas of rectangles will give a false impression. Of course, such a plot leaves space for interpretation.
A comparison of \(\small{t_\text{max}}\) was never – and is not – required by the FDA and Health Canada.
Whereas the underlying distribution of \(\small{t_\text{max}}\) is continuous, due to the sampling schedule the observed distribution is discrete. This calls for a comparison by a robust (nonparametric) statistical method.
In Europe a comparison by a nonparametric method was recommended for 19 years.7 8 That was – and still is! – statistically sound. A nonparametric method is currently recommended in some jurisdictions (e.g., Argentina,15 Japan,16 17 and South Africa18).
For modified release products \(\small{t_\text{max}}\) was not mentioned in the European Note for Guidance of 1999 at all.19
Alas, the EMA’s vague recommendation of 2010 was incurred in numerous other jurisdictions (e.g., Australia,20 ASEAN states,21 Chile,22 the EEU,23 Egypt,24 members of the Gulf Cooperation Council,25 New Zealand26).
The WHO leaves more scope for interpretation.
“Where \(\small{t_\text{max}}\) is considered clinically relevant, median and range of \(\small{t_\text{max}}\) should be compared between test and comparator to exclude numerical differences with clinical importance. A formal statistical comparison is rarely necessary. Generally the sample size is not calculated to have enough statistical power for \(\small{t_\text{max}}\). However, if \(\small{t_\text{max}}\) is to be subjected to a statistical analysis, this should be based on non-parametric methods and should be applied to untransformed data.
Problem Statement
- »A [formal] statistical evaluation of tmax is not
required.«
- Well. Does that imply that if one is performed anyhow, it is not welcomed?
- » […] there should be no apparent difference in median
tmax and its
variability
between test and reference product.«
- Leaving the dubious statement about an ‘apparent’ difference aside –
what might the ‘variability’ of the median be? The median is a statistic (one of
many estimators)
whose value is a certain number (the estimate).
To be clear: The median simply does not possess any ‘variability’.
If we agree that tmax follows a discrete distribution,28 we can only make a statement about the variability of the sample.29 A nonparametric statistic is the Interquartile Range (IQR). Is that meant?
- Leaving the dubious statement about an ‘apparent’ difference aside –
what might the ‘variability’ of the median be? The median is a statistic (one of
many estimators)
whose value is a certain number (the estimate).
To be clear: The median simply does not possess any ‘variability’.
- » […] there should be no apparent difference in median
tmax and its
range between test and reference product.«
- Similarly the median does not have a range, only the sample. At least the range is a statistical term we can work with.
- »Comparable median (≤ 20 % difference) […] Tmax.«
- This approach is statistically questionable at least.
- »Comparable […] range for Tmax.«
- What’s comparable?
Interlude: Scales and Distributions
Temperature in ℃ follows a continuous distribution on an interval scale. Say, we want to compare 10 ℃ with 20 ℃. Is 10 ℃ 50 % of 20 ℃? Of course, that’s absurd. What about 0 ℃ or –10 ℃? Calculating a ratio is not an allowed operation for data on an interval scale (i.e., with an arbitrary zero point). We must only add or subtract values. While saying that 10 ℃ is 10 ℃ less than 20 ℃ may sound trivial, it is definitely correct.
Compare that to the absolute temperature in Kelvin. It follows a continuous distribution on a ratio scale (i.e., with a true zero). Hence, beside adding/subtracting we are also allowed to multiply/divide values. Coming back to the example: Saying that 283 K (10 ℃) is 96.6 % of 293 K (20 ℃) is absolutely [sic] correct.
One might argue that \(\small{t_\text{max}}\) has a true zero as well and hence, is on a ratio scale. That’s valid for the true (but unknown) \(\small{t_\text{max}}\), which follows a continuous distribution. However, observed values follow a discrete distribution. Furthermore, it’s unlikely that all sampling intervals are equally spaced and therefore, calculating a ratio might be questionable.30 An option would be to sample in equally spaced intervals until absorption is essentially complete (in a one compartment model \(\small{\approx 2\times t_\textrm{max}}\)), divide the subject’s \(\small{t_\text{max}}\) by the sampling interval to obtain a positive integer, and analyze the counts as a Poisson distribution. However, the power of such an approach is poor.31
I doubt that calculating a percentage (even if allowed) is a good idea: Would you prefer to read in a report»\(\small{t_\text{max}}\) of test was 83.3 % of the reference«
or rather»\(\small{t_\text{max}}\) of test was observed 20 minutes earlier than the one of the reference«?
Of course, the ‘Two Lászlós’ explored how \(\small{t_\text{max}}\) behaves.
“The positive bias of \(\small{T_\textrm{max}}\) increase[s] together with the observational error. This result can be attributed to the asymmetry of the observed concentrations around the peak. The concentrations rise more steeply before the peak than they decline following the true maximum response. Consequently, it is more likely that large observed concentrations occur after than before the true peak time (\(\small{T^{\circ}_\textrm{max}}\)). “[…] the usefulness of peak times greatly diminishes when trying to characterize some MR formulations. Care must be taken when \(\small{T_\text{max}}\) (and \(\small{C_\text{max}}\)) is interpreted with concentration profiles having multiple peaks and MR preparations containing multiple components. Furthermore, the uncertainty of the recorded \(\small{T_\text{max}}\) renders it practically useless with the wide, almost flat peaks observed with extended-release formulations.
I could confirm the simulations32 33 by data from my archive (drug ‘X’, single dose, studies powered for the moderate variability of \(\small{C_\text{max}\textsf{)}}\).

Fig. 2 Pooled data of 7 studies (IR); red line median, red dashed lines 2.5 and 97.5 percentiles.
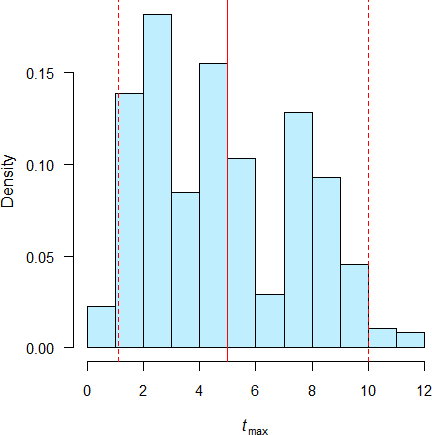
Fig. 3 Pooled data of 26 studies (MR); red line median, red dashed lines 2.5 and 97.5 percentiles.
I estimated the sample skewness by the method of moments \[g_1=\frac{\tfrac{1}{n} \sum_{i=1}^n (x_i-\overline{x})^3}{\sqrt{\tfrac{1}{n-1} \sum_{i=1}^n (x_i-\overline{x})^2}^{\,3}}.\tag{1}\] Obviously the distributions of \(\small{t_\text{max}}\) are skewed to the right (IR +0.778, MR +0.416) with a wide spread in the studies of MR formulations. Given that – and for comparing differences with the ±20 % criterion – couldn’t it make sense to use an asymmetrical acceptance range? More about that further down.
top of section ↩︎ previous section ↩︎
Basics
Imagine \(\small{x_{i=2}=\ldots=x_{i=n}}\) for \(\small{n\rightarrow \infty}\). If \(\small{x_1\rightarrow \infty}\) then \(\small{\bar{x}\rightarrow \infty}\). Hence, a single (‼) value distorts the mean towards the extreme. Therefore, the breakdown point of the arithmetic mean is 0. If any of the values is infinite, all others are practically ignored.
The median has a breakdown point of 0.5. That means, it would need
50 % of the data contaminated by ‘junk’ until the median of the sample
would change.34 Hence, it is a robust
estimator.
The breakdown point of the IQR
is 0.25.
On the other hand, the range has – like the mean – a breakdown point of 0. Therefore, it is not a robust statistic. Without inspecting the data or performing an EAD (e.g., box plots), the range is not informative and for comparisons completely useless.35
Imagine a study where all \(\small{t_\text{max}}\) values for three
treatments (R, T1, T2) were 1.
However, in one case after R it was 2 and in one case after
T1 it was 3. Now what?
sum.np <- function(x) {
# Nonparametric summary:
# Remove Mean but keep eventual NAs, add IQR and Range
y <- summary(x)
if (length(y) == 6) {
y <- y[c(1:3, 5:6)]
}else {
y <- y[c(1:3, 5:7)]
}
names <- c(names(y), "IQR", "Range")
y[length(y) + 1] <- y[["3rd Qu."]] - y[["1st Qu."]]
y[length(y) + 1] <- y[["Max."]] - y[["Min."]]
y <- setNames(as.vector(y), names)
return(y)
}
HL <- function(x, na.action = na.omit) {
# Hodges-Lehmann estimator of x
if (!is.vector(x) || !is.numeric(x))
stop("'x' must be a numeric vector!")
x <- na.action(x)
y <- outer(x, x, '+')
return(median(y[row(y) >= col(y)]) / 2)
}
n <- 16
spl <- 0.5 # sampling every 30 minutes
R <- c(rep(1, n-1), 2)
sumR <- sum.np(R)
T1 <- c(rep(1, n-1), 3)
sumT1 <- sum.np(T1)
T2 <- c(rep(1, n-1), 1)
sumT2 <- sum.np(T2)
hl <- c(HL(R), HL(T1), HL(T2))
comp1 <- data.frame(tmax = c(R, T1),
treatment = factor(rep(c("R", "T1"), c(n, n))))
comp2 <- data.frame(tmax = c(R, T2),
treatment = factor(rep(c("R", "T2"), c(n, n))))
res <- data.frame(treatment = c("R", "T1", "T2"),
Median = c(sumR[["Median"]], sumT1[["Median"]], sumT2[["Median"]]),
HL.est = hl,
IQR = c(sumR[["IQR"]], sumT1[["IQR"]], sumT2[["IQR"]]),
Range = c(sumR[["Range"]], sumT1[["Range"]], sumT2[["Range"]]))
# we need suppressWarnings() if data are identical
# (the CI cannot be computed)
wt1 <- suppressWarnings(
wilcox_test(tmax ~ treatment, data = comp1,
distribution = "exact", conf.int = TRUE,
conf.level = 0.90))
wt2 <- suppressWarnings(
wilcox_test(tmax ~ treatment, data = comp2,
distribution = "exact", conf.int = TRUE,
conf.level = 0.90))
p <- c(pvalue(wt1), pvalue(wt2))
PE <- c(suppressWarnings(confint(wt1)[[2]]),
suppressWarnings(confint(wt2)[[2]]))
lower <- c(suppressWarnings(confint(wt1)$conf.int[1]),
suppressWarnings(confint(wt2)$conf.int[1]))
upper <- c(suppressWarnings(confint(wt1)$conf.int[2]),
suppressWarnings(confint(wt2)$conf.int[2]))
wilc <- data.frame(comparison = c("T1 vs R", "T2 vs R"), p.value = p,
PE = PE, lower.CL = lower, upper.CL = upper)
wilc[, 2:5] <- signif(wilc[, 2:5], 4)
print(res, row.names = FALSE)
print(wilc, row.names = FALSE)# treatment Median HL.est IQR Range
# R 1 1 0 1
# T1 1 1 0 2
# T2 1 1 0 0
# comparison p.value PE lower.CL upper.CL
# T1 vs R 1 0 0 0
# T2 vs R 1 0 NA NANot only ‘apparently’ the medians and Hodges–Lehmann estimates are identical. The IQRs are funky.
Are the ranges ‘apparently’ different? I would say so. Is T1 inferior to R due to its wider range? Is T2 superior to R due to its narrower range? IMHO, such a comparision doesn’t make sense.
No significant differences are detected with a nonparametric test. Note that in the second comparison the confidence interval cannot be computed because all values of T2 are identical.
Interested in a more ‘realistic’ example? 48 subjects, sampling every 20 minutes between 40 and 100 minutes post dose. As above R ‘contaminated’ with one \(\small{t_\text{max}}\) value of two hours and T1 with one of three hours.
library(survival)
library(coin)
sum.np <- function(x) {
# Nonparametric summary:
# Remove Mean but keep eventual NAs, add IQR and Range
y <- summary(x)
if (length(y) == 6) {
y <- y[c(1:3, 5:6)]
}else {
y <- y[c(1:3, 5:7)]
}
names <- c(names(y), "IQR", "Range")
y[length(y) + 1] <- y[["3rd Qu."]] - y[["1st Qu."]]
y[length(y) + 1] <- y[["Max."]] - y[["Min."]]
y <- setNames(as.vector(y), names)
return(y)
}
HL <- function(x, na.action = na.omit) {
# Hodges-Lehmann estimator of x
if (!is.vector(x) || !is.numeric(x))
stop("'x' must be a numeric vector!")
x <- na.action(x)
y <- outer(x, x, '+')
return(median(y[row(y) >= col(y)]) / 2)
}
roundClosest <- function(x, y) {
# round x to the closest multiple of y
return(y * round(x / y))
}
set.seed(1234567) # for reproducibility
n <- 48
lo <- 40/60
hi <- 100/60
y <- 20/60
x <- runif(n - 1, min = lo, max = hi)
x <- roundClosest(x, y)
R <- c(x, 2)
x <- runif(n - 1, min = lo, max = hi)
x <- roundClosest(x, y)
T1 <- c(x, 3)
x <- runif(n - 1, min = lo, max = hi)
x <- roundClosest(x, y)
T2 <- c(x, 1)
sumR <- sum.np(R)
sumT1 <- sum.np(T1)
sumT2 <- sum.np(T2)
hl <- c(HL(R), HL(T1), HL(T2))
comp1 <- data.frame(tmax = c(R, T1),
treatment = factor(rep(c("R", "T1"), c(n, n))))
comp2 <- data.frame(tmax = c(R, T2),
treatment = factor(rep(c("R", "T2"), c(n, n))))
res <- data.frame(treatment = c("R", "T1", "T2"),
Median = c(sumR[["Median"]], sumT1[["Median"]], sumT2[["Median"]]),
HL.est = hl,
IQR = c(sumR[["IQR"]], sumT1[["IQR"]], sumT2[["IQR"]]),
Min = c(sumR[["Min."]], sumT1[["Min."]], sumT2[["Min."]]),
Max = c(sumR[["Max."]], sumT1[["Max."]], sumT2[["Max."]]),
Range = c(sumR[["Range"]], sumT1[["Range"]], sumT2[["Range"]]))
res[, 2:7] <- signif(res[, 2:7], 4)
wt1 <- wilcox_test(tmax ~ treatment, data = comp1,
distribution = "exact", conf.int = TRUE,
conf.level = 0.90)
wt2 <- wilcox_test(tmax ~ treatment, data = comp2,
distribution = "exact", conf.int = TRUE,
conf.level = 0.90)
p <- c(pvalue(wt1), pvalue(wt2))
PE <- c(confint(wt1)[[2]], confint(wt2)[[2]])
lower <- c(confint(wt1)$conf.int[1], confint(wt2)$conf.int[1])
upper <- c(confint(wt1)$conf.int[2], confint(wt2)$conf.int[2])
wilc <- data.frame(comparison = c("T1 vs R", "T2 vs R"), p.value = p,
PE = PE, lower.CL = lower, upper.CL = upper)
wilc[, 2:5] <- signif(wilc[, 2:5], 4)
# box plots
ylim <- 1.04 * c(0, max(c(R, T1, T2), na.rm = TRUE))
dev.new(width = 4.6, height = 4.6)
op <- par(no.readonly = TRUE)
par(mar = c(2.1, 4.1, 0, 0), cex.axis = 0.9)
plot(c(0.5, 3.5), c(0, 0), type = "n", axes = FALSE,
ylim = ylim, xlab = "", ylab = expression(italic(t)[max]))
axis(1, at = 1:3, labels = c("R", expression(T[1]), expression(T[2])), tick = FALSE)
axis(2, las = 1)
boxplot(tmax ~ treatment, data = comp1, add = TRUE, at = 1:2, boxwex = 0.4,
ylim = ylim, names = "", whisklty = 1, medcol = "mediumblue", main = "",
axes = FALSE, col = "lightblue1", outcol = "red")
boxplot(tmax ~ treatment, data = comp2, add = TRUE, at = c(1, 3), boxwex = 0.4,
ylim = ylim, names = "", ylab = "", whisklty = 1, medcol = "mediumblue",
main = "", axes = FALSE, col = "lightblue1", outcol = "red")
points(1:3, hl, col = "blue", pch = 19, cex = 1.15)
par(op)
print(res, row.names = FALSE)
print(wilc, row.names = FALSE)# treatment Median HL.est IQR Min Max Range
# R 1.333 1.167 0.3333 0.6667 2.000 1.333
# T1 1.000 1.167 0.3333 0.6667 3.000 2.333
# T2 1.333 1.167 0.3333 0.6667 1.667 1.000
# comparison p.value PE lower.CL upper.CL
# T1 vs R 0.1378 0 0 0.3333
# T2 vs R 0.4410 0 0 0.3333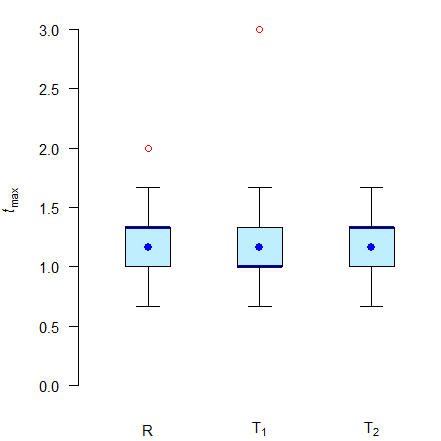
Fig. 4 Box plots of simulated \(\small{t_\text{max}}\) values.
Thick blue lines medians, filled blue circles Hodges-Lehmann estimates, red circles outliers.
Is the median of T1 with 60 minutes ‘apparently’ different
from the one of R with 75 minutes? If we would assess the median for a
±20 % difference,11 12 13
T1 would fail with its –25 %. Note that the Hodges-Lehmann
estimates of all three treatments are identical.
Since we contamined the data of R and T1, all ranges are
different. To be expected with the breakdown point of 0. The
IQRs are not affected by 2 % of
contaminated data due to the breakdown point of 0.25.
With a nonparametric test no significant differences (p
> 0.05) are detected; the confidence intervals include zero.
What might an almighty assessor conclude by looking at the medians or ranges?
Are they ‘apparently’ different?
Simulations
I selected a simple one. An immediate release formulation, one
compartment model, PK-parameters:
\(\small{D=100}\), fraction absorbed
\(\small{f=0.80}\), volume of
distribution \(\small{V=4}\),
absorption rate constant \(\small{k_{\,01}=2\,\textrm{h}^{-1}}\)
(\(\small{t_{1/2}\approx0.35\,\text{h}}\)),
lag time \(\small{t_\textrm{lag}=5\,\textrm{min}}\),
elimination rate constant \(\small{k_{\,10}=0.25\,\textrm{h}^{-1}}\)
(\(\small{t_{1/2}\approx2.77\,\text{h}}\)).
The sampling schedule was every 15 minutes until 2.5 hours, 3.25, 4.25,
5.5, 7, 9.25, and 12 hours in order to get a reliable estimate of \(\small{t_\text{max}}\) (the theoretical
value based on the model is 1.272 hours).
Error distributions were uniform
for \(\small{f}\) (0.6–1), log-normal
for \(\small{V}\) (CV 50 %),
\(\small{k_{\,01}}\) (CV
35 %), \(\small{k_{\,10}}\)
(CV 40 %), and truncated
normal for \(\small{t_\textrm{lag}}\) (limits 0–15 min).
Analytical error was log-normal with a CV of 5 % of the
simulated concentration.
25 simulated studies with 48 subjects each. The LLOQ was set to 5 % of the theoretical \(\small{C_\text{max}}\).
I split the data of the studies in halves (mimicking a parallel design with 24 subjects / treatment arm) and compared the medians, interquartile ranges, and ranges. Furthermore, I compared the \(\small{t_\text{max}}\) values by the Mann–Whitney U (aka Wilcoxon-Mann-Whitney) test.36 Cave: 192 LOC.
library(truncnorm)
library(reshape)
library(survival)
library(coin)
library(lattice)
sum.np <- function(x) {
# Nonparametric summary:
# Remove Mean but keep eventual NAs, add IQR and Range
y <- summary(x)
if (length(y) == 6) {
y <- y[c(1:3, 5:6)]
}else {
y <- y[c(1:3, 5:7)]
}
names <- c(names(y), "IQR", "Range")
y[length(y) + 1] <- y[["3rd Qu."]] - y[["1st Qu."]]
y[length(y) + 1] <- y[["Max."]] - y[["Min."]]
y <- setNames(as.vector(y), names)
return(y)
}
HL <- function(x, na.action = na.omit) {
# Hodges-Lehmann estimator of x
if (!is.vector(x) || !is.numeric(x))
stop("'x' must be a numeric vector!")
x <- na.action(x)
y <- outer(x, x, '+')
return(median(y[row(y) >= col(y)]) / 2)
}
Ct <- function(x, D = D, F = F.d, V = V.d,
k01 = k01.d, k10 = k10.d, tlag = tlag.d) {
# one-compartment model with a lag time
C <- F.d * D * k01 / (V.d * (k01 - k10.d)) *
(exp(-k10 *(x - tlag)) - exp(-k01 * (x - tlag)))
C[C < 0] <- 0
return(C)
}
set.seed(123456)
delta <- 20/60 # clinically relevant difference (20 minutes)
spl <- 0.25 # early interval (up to ~2× theoretical tmax)
early <- cumsum(rep(spl, 10))
t <- c(0, early, 3.25, 4.25, 5.5, 7, 9.25, 12)
studies <- 25 # number of studies
n <- 48 # number of subjects / study (must be even)
D <- 100 # dose
# Index ".d" denotes theoretical value, ".c" its CV
F.d <- 0.8 # fraction absorbed
F.l <- 0.6 # lower limit
F.u <- 1 # upper limit
V.d <- 4 # volume of distribution
V.c <- 0.50 # CV 50%, lognormal
k01.d <- 2 # absorption rate constant
k01.c <- 0.35 # CV 35%, lognormal
k10.d <- 0.25 # elimination rate constant
k10.c <- 0.40 # CV 40%, lognormal
tlag.d <- 5/60 # lag time
tlag.l <- 0 # lower truncation 1
tlag.u <- 0.25 # upper truncation 1
tlag.c <- 0.5 # CV 50%, truncated normal
AErr <- 0.05 # analytical error CV 5%, lognormal
LLOQ.f <- 0.05 # fraction of theoretical Cmax
# theoretical profile
x <- seq(min(t), max(t), length.out=2500)
C.th <- Ct(x = x, D = D, F = F.d, V = V.d,
k01 = k01.d, k10 = k10.d, tlag = tlag.d)
tmax <- log(k01.d / k10.d) / (k01.d - k10.d) + tlag.d
Cmax <- Ct(x = tmax, D = D, F = F.d, V = V.d,
k01 = k01.d, k10 = k10.d, tlag = tlag.d)
LLOQ <- LLOQ.f * Cmax
data <- data.frame(study = rep(1:studies, each = n * length(t)),
subject = rep(1:n, each = length(t)),
t = t, C = NA)
for (study in 1:studies) {
# individual PK parameters
F <- runif(n = n, min = F.l, max = F.u)
V <- rlnorm(n = n, meanlog = log(V.d) - 0.5 * log(V.c^2 + 1),
sdlog = sqrt(log(V.c^2 + 1)))
k01 <- rlnorm(n = n, meanlog = log(k01.d) - 0.5 * log(k01.c^2 + 1),
sdlog = sqrt(log(k01.c^2 + 1)))
k10 <- rlnorm(n = n, meanlog = log(k10.d) - 0.5 * log(k10.c^2 + 1),
sdlog = sqrt(log(k10.c^2 + 1)))
tlag <- rtruncnorm(n = n, a = tlag.l, b = tlag.u,
mean = tlag.d, sd = tlag.c)
for (subject in 1:n) {
# individual profiles
C <- Ct(x = t, D = D, F = F[subject], V = V[subject],
k01 = k01[subject], k10 = k10[subject],
tlag = tlag[subject])
for (k in 1:length(t)) {# analytical error (multiplicative)
if (k == 1) {
AErr1 <- rnorm(n = 1, mean = 0, sd = abs(C[k] * AErr))
}else {
AErr1 <- c(AErr1, rnorm(n = 1, mean = 0, sd = abs(C[k] * AErr)))
}
}
C <- C + AErr1 # add analytical error
C[C < LLOQ] <- NA # assign NAs to Cs below LLOQ
data$C[data$study == study & data$subject == subject] <- C
}
}
# simple NCA
res <- data.frame(study = rep(1:studies, each = n),
subject = rep(1:n, studies),
tlag = NA, tmax = NA, Cmax = NA)
i <- 0
for (j in 1:studies) {
for (k in 1:n) {
i <- i + 1
tmp.t <- data$t[data$study == j & data$subject == k]
tmp.C <- data$C[data$study == j & data$subject == k]
res$tlag[i] <- tmp.t[which(tmp.t == t[!is.na(tmp.C)][1])+1]
res$Cmax[i] <- max(tmp.C, na.rm = TRUE)
res$tmax[i] <- tmp.t[which(tmp.C == res$Cmax[i])]
}
}
comp <- data.frame(study = 1:studies, med.T = NA, med.R = NA, ratio = NA,
IQR.T = NA, IQR.R = NA, rg.T = NA, rg.R = NA,
CL.lo = NA, CL.hi = NA, pass.ratio = FALSE,
pass.CI = FALSE, hl.T = NA, hl.R = NA)
for (i in 1:studies) {
study <- res[res$study == i, ]
sum.T <- sum.np(study$tmax[study$subject == 1:(n/2)])
sum.R <- sum.np(study$tmax[study$subject == (n/2+1):n])
comp$med.T[i] <- sum.T[["Median"]]
comp$med.R[i] <- sum.R[["Median"]]
comp$ratio[i] <- signif(comp$med.T[i] / comp$med.R[i], 4)
comp$IQR.T[i] <- sum.T[["IQR"]]
comp$IQR.R[i] <- sum.R[["IQR"]]
comp$rg.T[i] <- sum.T[["Range"]]
comp$rg.R[i] <- sum.R[["Range"]]
if (comp$ratio[i] >= 0.8 & comp$ratio[i] <= 1.2) comp$pass.ratio[i] <- TRUE
stud.tmax <- data.frame(tmax = study$tmax,
part = factor(rep(c("R", "T"), c(n/2, n/2))))
wt <- wilcox_test(tmax ~ part, data = stud.tmax,
distribution = "exact", conf.int = TRUE,
conf.level = 0.90)
comp$CL.lo[i] <- confint(wt)$conf.int[1]
comp$CL.hi[i] <- confint(wt)$conf.int[2]
if (abs(comp$CL.lo[i]) <= delta & abs(comp$CL.lo[i]) <= delta)
comp$pass.CI[i] <- TRUE
comp$hl.T[i] <- HL(study$tmax[study$subject == 1:(n/2)])
comp$hl.R[i] <- HL(study$tmax[study$subject == (n/2+1):n])
}
comp$CL.lo <- sprintf("%+.2f", comp$CL.lo)
comp$CL.hi <- sprintf("%+.2f", comp$CL.hi)
for (i in 1:studies) {# cosmetics
if (comp$CL.lo[i] == "+0.00") comp$CL.lo[i] <- "\u00B10.00"
if (comp$CL.hi[i] == "+0.00") comp$CL.hi[i] <- "\u00B10.00"
}
diff.med <- sprintf("%+.0f min", 60 * range(comp$med.T - comp$med.R, na.rm = TRUE))
diff.rat <- sprintf("%.4f", range(comp$ratio))
diff.iqr <- sprintf("%+.0f min", 60 * range(comp$IQR.T - comp$IQR.R, na.rm = TRUE))
diff.rge <- sprintf("%+.0f min", 60 * range(comp$rg.T - comp$rg.R, na.rm = TRUE))
txt <- paste("\nDifferences of medians:", paste(diff.med, collapse = " to "),
"\nMedian ratios : ", paste(diff.rat, collapse = " to "),
"\nDifferences of IQRs :", paste(diff.iqr, collapse = " to "),
"\nDifferences of ranges :", paste(diff.rge, collapse = " to "),
"\nPassed CI inclusion :", sprintf("%6.2f%%",
100 * sum(comp$pass.CI) /
studies),
"\nPassed \u00B120% difference:", sprintf("%6.2f%%",
100 * sum(comp$pass.ratio) /
studies))
print(comp[, 1:10], row.names = FALSE)
cat(txt)
prep <- as.data.frame(
melt(res, id = c("study", "subject"), measure = "tmax"))
for (i in 1:nrow(prep)) {
if (prep$subject[i] %in% 1:(n/2)) {
prep$group[i] <- "Test"
}else {
prep$group[i] <- "Reference"
}
}
prep$study <- as.factor(prep$study)
prep$subject <- as.factor(prep$subject)
prep$group <- as.factor(prep$group)
# box plots
dev.new(width = 6, height = 6)
op <- par(no.readonly = TRUE)
trellis.par.set(box.umbrella = list(lty = 1))
trellis.par.set(box.dot = list(cex = 0.82, col = "#0000BB"))
bwplot(value ~ study | variable*group, data = prep, group = group,
xlab = "study", ylab = "hours", ylim = 1.04 * c(0, max(res$tmax)),
panel=function(...) {
panel.bwplot(...)
panel.points(x = c(comp$hl.T, comp$hl.R)[1:n],
pch = 21, cex = 0.6,
col = "red", fill = "#BB000080")
}
)
par(op)# study med.T med.R ratio IQR.T IQR.R rg.T rg.R CL.lo CL.hi
# 1 1.500 1.500 1.0000 0.5000 0.5625 1.50 1.50 -0.25 +0.25
# 2 1.500 1.375 1.0910 0.3125 0.3125 1.00 1.50 -0.25 +0.25
# 3 1.250 1.500 0.8333 0.2500 0.5000 1.50 1.25 -0.25 ±0.00
# 4 1.500 1.500 1.0000 0.3125 0.5000 1.25 1.75 -0.25 +0.25
# 5 1.500 1.250 1.2000 0.5000 0.7500 1.75 1.50 ±0.00 +0.50
# 6 1.375 1.500 0.9167 0.5625 0.5000 1.50 1.50 -0.25 ±0.00
# 7 1.625 1.500 1.0830 1.0000 0.6250 2.50 1.50 -0.25 +0.25
# 8 1.500 1.250 1.2000 0.5000 0.5625 1.25 1.50 -0.25 +0.25
# 9 1.250 1.375 0.9091 0.5625 0.7500 2.00 1.50 -0.25 ±0.00
# 10 1.500 1.500 1.0000 0.5000 0.5000 1.25 1.25 ±0.00 +0.25
# 11 1.250 1.500 0.8333 0.5000 0.5625 1.75 1.25 -0.50 ±0.00
# 12 1.500 1.500 1.0000 0.5625 0.7500 1.50 1.25 ±0.00 +0.50
# 13 1.250 1.750 0.7143 0.3125 0.7500 1.50 1.50 -0.50 ±0.00
# 14 1.250 1.750 0.7143 0.5000 0.8125 1.50 1.25 -0.50 ±0.00
# 15 1.500 1.250 1.2000 0.7500 0.2500 1.50 1.25 ±0.00 +0.50
# 16 1.500 1.500 1.0000 0.5000 0.5625 2.25 1.50 -0.25 +0.25
# 17 1.500 1.375 1.0910 0.5000 0.5000 1.75 1.50 -0.25 +0.25
# 18 1.250 1.500 0.8333 0.5625 0.5000 1.75 1.50 -0.25 ±0.00
# 19 1.750 1.500 1.1670 0.7500 0.5625 1.00 1.50 ±0.00 +0.25
# 20 1.500 1.500 1.0000 0.2500 0.5000 1.75 1.75 -0.25 ±0.00
# 21 1.250 1.250 1.0000 0.5000 0.2500 2.50 1.50 ±0.00 +0.25
# 22 1.500 1.375 1.0910 0.7500 0.5000 1.75 1.50 -0.25 +0.25
# 23 1.375 1.500 0.9167 0.7500 0.5625 1.25 1.75 -0.25 ±0.00
# 24 1.250 1.375 0.9091 0.2500 0.3125 1.50 1.25 -0.25 +0.25
# 25 1.500 1.500 1.0000 0.5625 0.5000 2.50 1.50 -0.25 +0.25
#
# Differences of medians: -30 min to +15 min
# Median ratios : 0.7143 to 1.2000
# Differences of IQRs : -26 min to +30 min
# Differences of ranges : -30 min to +60 min
# Passed CI inclusion : 88.00%
# Passed ±20% difference: 92.00%
Blue circles medians, small red circles Hodges-Lehmann estimates.
Note that in three cases \(\small{t_\text{max}}\) was observed at 3.25 hours because the tight sampling ended at 2.5 hours. Try to modify the script with
early <- cumsum(rep(spl, 12))More studies woul pass because we get more accurate estimates.
In a real study – if \(\small{t_\text{max}}\) is a clinically relevant PK metric – one would have to pre-specify the acceptance limits and assess whether the ≈90% CI lies entirely within. For an analgesic for rapid relief of pain it might be as short as ±20 minutes. If this would have been the case in the example above, four studies would fail because the CI is not entirely with the acceptance range. Here the ±20 % criterion is more permissive; only two studies would fail.
However, if we follow the current guidelines we are left in the dark.
- Is a difference in medians of –30 minutes or +15 minutes
‘apparent’ ?
No idea. - Even worse the interquartile ranges. Here we have values from –26 to
+30 minutes.
Are they ‘apparently’ different? - Let’s forget the range, please.
What might –30 minutes to +1 hour tell us?
Let’s evaluate the simulated studies by the nonparametric approach proposed by Basson et al.31 (fitting a generalized linear model with a Poisson error distribution).
# requires the result of the simulation script
alpha <- 0.05
df <- prep[, c(1, 4:5)]
names(df)[2:3] <- c("tmax", "treatment")
comp1 <- data.frame(study = 1:studies, Estim.T = NA, Estim.R = NA,
delta = NA, p.value = NA, pass = FALSE)
# convert tmax to counts
df$count <- as.integer(df$tmax / spl)
for (study in 1:studies) {
tmp <- df[df$study == study, ]
m <- glm(count ~ treatment, data = tmp, family = "poisson")
smry <- summary(m)
# estimated counts in log-scale
T <- smry$coeff[["(Intercept)", "Estimate"]] +
smry$coeff[["treatmentTest", "Estimate"]]
R <- smry$coeff[["(Intercept)", "Estimate"]] -
smry$coeff[["treatmentTest", "Estimate"]]
# back-convert estimated counts to tmax
comp1$Estim.T[study] <- exp(T) * spl
comp1$Estim.R[study] <- exp(R) * spl
comp1$delta[study] <- comp1$Estim.T[study] - comp1$Estim.R[study]
comp1$p.value[study] <- smry$coeff[["treatmentTest", "Pr(>|z|)"]]
if (comp1$p.value[study] >= alpha) comp1$pass[study] <- TRUE
}
comp1[, c(1:2, 5)] <- round(comp1[, c(1:2, 5)], 5)
comp1[, 4] <- sprintf("%+.5f", comp1[, 4])
for (i in 1:studies) {# cosmetics
if (comp1[i, 4] == "-0.00000" | comp1[i, 4] == "+0.00000")
comp1[i, 4] <- "\u00B10.00000"
}
print(comp1, row.names = FALSE)# study Estim.T Estim.R delta p.value pass
# 1 1.52083 1.562785 -0.04195 0.90714 TRUE
# 2 1.41667 1.522748 -0.10608 0.76387 TRUE
# 3 1.36458 1.694975 -0.33039 0.36768 TRUE
# 4 1.47917 1.479167 ±0.00000 1.00000 TRUE
# 5 1.59375 1.222495 +0.37126 0.26241 TRUE
# 6 1.41667 1.655101 -0.23843 0.51329 TRUE
# 7 1.62500 1.442909 +0.18209 0.60518 TRUE
# 8 1.41667 1.395910 +0.02076 0.95156 TRUE
# 9 1.37500 1.546717 -0.17172 0.62768 TRUE
# 10 1.51042 1.388003 +0.12241 0.72183 TRUE
# 11 1.34375 1.890262 -0.54651 0.15345 TRUE
# 12 1.59375 1.204316 +0.38943 0.23734 TRUE
# 13 1.33333 2.083333 -0.75000 0.05988 TRUE
# 14 1.35417 1.661538 -0.30737 0.39789 TRUE
# 15 1.60417 1.251082 +0.35308 0.29082 TRUE
# 16 1.56250 1.646944 -0.08444 0.81855 TRUE
# 17 1.48958 1.327579 +0.16200 0.63141 TRUE
# 18 1.38542 1.491541 -0.10612 0.76135 TRUE
# 19 1.58333 1.343202 +0.24013 0.48265 TRUE
# 20 1.44792 1.641487 -0.19357 0.59530 TRUE
# 21 1.44792 1.286046 +0.16187 0.62640 TRUE
# 22 1.53125 1.388889 +0.14236 0.67949 TRUE
# 23 1.43750 1.653382 -0.21588 0.55439 TRUE
# 24 1.43750 1.375679 +0.06182 0.85592 TRUE
# 25 1.60417 1.521916 +0.08225 0.81855 TRUEIn none of the studies a significant difference was detected at the 0.05 level and hence, all would pass. Study 13 showed the largest difference of \(\small{t_\text{max}}\) values and with 0.05988 the lowest p-value. As we have seen above, it failed the ±20 % criterion as well as the CI inclusion approach.
Interlude: Exploring the ±20 % criterion
Let’s dive deeper into the murky waters.11 12 13
One compartment model,
PK-parameters: \(\small{D=100}\), fraction absorbed \(\small{f=0.80}\), volume of distribution
\(\small{V=4}\), elimination half life
4 hours. Three formulations: A (‘fast’ test) and B (‘slow’ test)
compared to R (reference). The absorption rate constants are optimized
in such a way that \(\small{t_\text{max(A)}=0.8\,\text{h}}\),
\(\small{t_\text{max(B)}=1.2\,\text{h}}\),
and \(\small{t_\text{max(R)}=1\,\text{h}}\). The
sampling schedule was every 5 (five!) minutes until two hours
(i.e., \(\small{2\times
t_\text{max(R)}}\)), 2.25, 2.5, 3, 3.5, 4, 6, 9, 12, and 16 hours
(34 time points). Error distributions were uniform
for \(\small{f}\) (0.6–1), log-normal
for \(\small{V}\) (CV 50 %),
\(\small{k_{\,01}}\)
(CV 35 %), and \(\small{k_{\,10}}\) (CV 40 %).
Distribution of the analytical error was normal with
a CV of 5 % of the simulated concentration. The
LLOQ was set to 5 %
of \(\small{C_\text{max(R)}}\).
Simulated parallel designs with 24 subjects in each of the three
treatment arms. Although the \(\small{t_\text{max}\textsf{-}}\)values of
treatments A (fast) and B (slow) are at the borders of the ±20 %
criterion, this is not a statistical test and hence, it is
impossible to explore the empiric Type I Error. At least the number of
passing studies divided by the number of simulations should give us an
impression what might happen. Naïvely we expect that 50 % would pass,
right?
There should be an equal chance that \(\small{\widetilde{t}_\text{max(A)}<0.8\times\widetilde{t}_\text{max(R)}}\)
and \(\small{\widetilde{t}_\text{max(A)}\geq0.8\times\widetilde{t}_\text{max(R)}}\)
as well as \(\small{\widetilde{t}_\text{max(B)}\leq1.2\times\widetilde{t}_\text{max(R)}}\)
and \(\small{\widetilde{t}_\text{max(B)}>1.2\times\widetilde{t}_\text{max(R)}}\).
Contrary to this hocuspocus we can perform the Mann–Whitney
U (aka
Wilcoxon-Mann-Whitney) test at level \(\small{\alpha}\) and assess the studies
based on the \(\small{100\,(1-2\,\alpha)}\) confidence
inclusion approach \[\begin{array}{c}
\theta_1=-\Delta\:\small{\textsf{and}}\:\theta_2=+\Delta\\
H_0:\mu_\textrm{T}-\mu_\textrm{R}\not\subset\left\{\theta_1,\,\theta_2\right\}\;vs\;H_1:\theta_1<\mu_\textrm{T}-\mu_\textrm{R}<\theta_2
\end{array}\tag{2}\] based on a pre-specified
clinically relevant difference \(\small{\Delta}\) (in the example \(\small{\Delta=0.2\,\text{h}}\)).
Since \(\small{\mu_\textrm{T(A)}=\theta_1}\) and
\(\small{\mu_\textrm{T(B)}=\theta_2}\),
we expect for \(\small{\alpha=0.05}\)
that 5 % of both treatments will fail.
# Cave: long runtime (1,000 simulations take 30 minutes on my aged machine)
library(moments)
library(survival)
library(coin)
opt <- function(x, k10.d, tmax) {
# absorption rate constant for given elimination at tmax
log(x / k10.d) / (x - k10.d) - tmax
}
Ct <- function(D = D, F = F.d, V = V.d, k01 = k01.d, k10 = k10.d, t) {
# one-compartment model, no lag time
if (!isTRUE(all.equal(k01, k10))) {# common: k01 != k10
C <- F * D * k01 / (V * (k01 - k10)) * (exp(-k10 * t) - exp(-k01 * t))
}else { # flip-flop PK
k <- k10
C <- F * D / V * k * t * exp(-k * t)
}
return(C)
}
progr <- FALSE # in your own simulations set to TRUE
alpha <- 0.05 # level of the test
tmax <- setNames(c(1, 0.8, 1.2), c("R", "A", "B"))
studies <- 2500 # number of simulated studies
n <- 24 # number of subjects in each arm of a study
delta <- c(-20, +20) # acceptable differences (%)
# limits for the median of test / reference
limit <- signif((100 + delta) / 100, 9)
# limits for the confidence interval inclusion approach
# note: rounding to 9 significant digits because issues with
# numeric precision in the comparison
theta1 <- signif(tmax[["A"]] - tmax[["R"]], 9)
theta2 <- signif(tmax[["B"]] - tmax[["R"]], 9)
D <- 100 # dose
# Index ".d" denotes theoretical value, ".c" its CV
F.d <- 0.8 # fraction absorbed
F.l <- 0.6 # lower limit
F.u <- 1 # upper limit
V.d <- 4 # volume of distribution
V.c <- 0.50 # CV 50% (lognormal)
k10.d <- log(2) / 4 # elimination rate constant (equal for T and R)
k10.c <- 0.40 # CV 40% (lognormal)
# absorption rate constants
k01.dR <- uniroot(opt, interval = c(0, 24), tol = 1e-8,
k10.d = k10.d, tmax = tmax[["R"]])$root # R
k01.dA <- uniroot(opt, interval = c(0, 24), tol = 1e-8,
k10.d = k10.d, tmax = tmax[["A"]])$root # A (fast)
k01.dB <- uniroot(opt, interval = c(0, 24), tol = 1e-8,
k10.d = k10.d, tmax = tmax[["B"]])$root # B (slow)
k01.c <- 0.35 # CV 35% (lognormal)
AErr <- 0.05 # analytical error CV 5% (normal)
LLOQ.f <- 0.05 # fraction of theoretical Cmax
Cmax.R <- Ct(D, F.d, V.d, k01.dR, k10.d, tmax[["R"]])
LLOQ <- LLOQ.f * Cmax.R
t <- sort(unique(c(seq(0, 2 * tmax[["R"]], 5 / 60),
2.25, 2.5, 3, 3.5, 4, 6, 9, 12, 16)))
R <- A <- B <- data.frame(study = rep(1:studies, each = n * length(t)),
subject = rep(1:n, each = length(t)), t = t, C = NA_real_)
res.R <- res.A <- res.B <- data.frame(study = rep(1:studies, each = n),
subject = rep(1:n, studies),
tmax = NA_real_)
comp <- data.frame(study = 1:studies, median.R = NA_real_, median.A = NA_real_,
median.B = NA_real_, ratio.AR = NA_real_, ratio.BR = NA_real_,
pass.A = FALSE, pass.B = FALSE, pass.CL.A = FALSE,
pass.CL.B = FALSE)
set.seed(123456) # for reproducibility
if (progr) pb <- txtProgressBar(0, 1, 0, width = NA, style = 3)
for (study in 1:studies) {# subject’s PK parameters & profiles
for (subject in 1:n) {
F <- runif(n = 1, min = F.l, max = F.u)
V <- rlnorm(n = 1, meanlog = log(V.d) - 0.5 * log(V.c^2 + 1),
sdlog = sqrt(log(V.c^2 + 1)))
k01.Rs <- rlnorm(n = 1, meanlog = log(k01.dR) - 0.5 * log(k01.c^2 + 1),
sdlog = sqrt(log(k01.c^2 + 1)))
k01.As <- rlnorm(n = 1, meanlog = log(k01.dA) - 0.5 * log(k01.c^2 + 1),
sdlog = sqrt(log(k01.c^2 + 1)))
k01.Bs <- rlnorm(n = 1, meanlog = log(k01.dB) - 0.5 * log(k01.c^2 + 1),
sdlog = sqrt(log(k01.c^2 + 1)))
k10s <- rlnorm(n = 1, meanlog = log(k10.d) - 0.5 * log(k10.c^2 + 1),
sdlog = sqrt(log(k10.c^2 + 1)))
C.R <- Ct(D, F = F, V = V, k01 = k01.Rs, k10 = k10s, t)
C.A <- Ct(D, F = F, V = V, k01 = k01.As, k10 = k10s, t)
C.B <- Ct(D, F = F, V = V, k01 = k01.Bs, k10 = k10s, t)
# add analytical error (normal)
C.R <- C.R + rnorm(n = length(t), mean = 0, sd = abs(C.R * AErr))
C.A <- C.A + rnorm(n = length(t), mean = 0, sd = abs(C.A * AErr))
C.B <- C.B + rnorm(n = length(t), mean = 0, sd = abs(C.B * AErr))
# assign NAs to Cs below LLOQ
C.R[C.R < LLOQ] <- NA
C.A[C.A < LLOQ] <- NA
C.B[C.B < LLOQ] <- NA
# set NAs before tmax to zero
tmax.R <- t[which(C.R == max(C.R, na.rm = TRUE))]
tmax.A <- t[which(C.A == max(C.A, na.rm = TRUE))]
tmax.B <- t[which(C.B == max(C.B, na.rm = TRUE))]
C.R[which(t[which(is.na(C.R))] < tmax.R)] <- 0
C.A[which(t[which(is.na(C.A))] < tmax.A)] <- 0
C.B[which(t[which(is.na(C.B))] < tmax.B)] <- 0
R$C[R$study == study & R$subject == subject] <- C.R
A$C[A$study == study & A$subject == subject] <- C.A
B$C[B$study == study & B$subject == subject] <- C.B
res.R$tmax[res.R$study == study & res.R$subject == subject] <- tmax.R
res.A$tmax[res.A$study == study & res.A$subject == subject] <- tmax.A
res.B$tmax[res.B$study == study & res.B$subject == subject] <- tmax.B
}
comp$median.R[study] <- median(res.R$tmax[res.R$study == study], na.rm = TRUE)
comp$median.A[study] <- median(res.A$tmax[res.A$study == study], na.rm = TRUE)
comp$median.B[study] <- median(res.B$tmax[res.B$study == study], na.rm = TRUE)
comp$ratio.AR[study] <- comp$median.A[study] / comp$median.R[study]
comp$ratio.BR[study] <- comp$median.B[study] / comp$median.R[study]
if (comp$ratio.AR[study] >= limit[1] & comp$ratio.AR[study] <= limit[2])
comp$pass.A[study] <- TRUE
if (comp$ratio.BR[study] >= limit[1] & comp$ratio.BR[study] <= limit[2])
comp$pass.B[study] <- TRUE
# 90% confidence intervals of the Wilcoxon-Mann-Whitney test
tmax.R.res <- res.R[res.R$study == study, "tmax"]
tmax.AR <- data.frame(tmax = c(res.A[res.A$study == study, "tmax"],
tmax.R.res),
treatment = factor(rep(c("R", "T"), c(n, n))))
CI.AR <- signif(as.numeric(unlist(
confint(wilcox_test(tmax ~ rev(treatment),
data = tmax.AR,
distribution = "exact",
conf.int = TRUE,
conf.level = 1 - 2 * alpha))[1])), 9)
tmax.BR <- data.frame(tmax = c(res.B[res.B$study == study, "tmax"],
tmax.R.res),
treatment = factor(rep(c("T", "R"), c(n, n))))
CI.BR <- signif(as.numeric(unlist(
confint(wilcox_test(tmax ~ rev(treatment),
data = tmax.BR,
distribution = "exact",
conf.int = TRUE,
conf.level = 1 - 2 * alpha))[1])), 9)
if (CI.AR[1] >= theta1 & CI.AR[2] <= theta2) comp$pass.CL.A[study] <- TRUE
if (CI.BR[1] >= theta1 & CI.BR[2] <= theta2) comp$pass.CL.B[study] <- TRUE
if (progr) setTxtProgressBar(pb, study / studies)
} # patience please...
if (progr) close(pb)
cat("Simulation settings",
paste0("\n ", formatC(studies, format = "d", big.mark = ","),
" studies (", n, " subjects / arm)"),
"\n tmax (A = fast) :", sprintf("%.4f h", tmax[["A"]]),
sprintf("(t½,a: %.2f min)", 60 * log(2) / k01.dA),
"\n tmax (B = slow) :", sprintf("%.4f h", tmax[["B"]]),
sprintf("(t½,a: %.2f min)", 60 * log(2) / k01.dB),
"\n tmax (Reference):", sprintf("%.4f h", tmax[["R"]]),
sprintf("(t½,a: %.2f min)", 60 * log(2) / k01.dR),
"\n\nSimulation results",
"\n A = fast",
paste0("\n Range : ",
paste(sprintf("%.4f",
range(res.A$tmax, na.rm = TRUE)), collapse = " h, "), " h"),
paste0("\n Skewness: ", sprintf("%+.4f", skewness(res.A$tmax))),
"\n B = slow",
paste0("\n Range : ",
paste(sprintf("%.4f",
range(res.B$tmax, na.rm = TRUE)), collapse = " h, "), " h"),
paste0("\n Skewness: ", sprintf("%+.4f", skewness(res.B$tmax))),
"\n Reference",
paste0("\n Range : ",
paste(sprintf("%.4f",
range(res.R$tmax, na.rm = TRUE)), collapse = " h, "), " h"),
paste0("\n Skewness: ", sprintf("%+.4f", skewness(res.R$tmax))),
"\n\n A = fast passed ±20% criterion :",
sprintf("%.1f%%", 100 * sum(comp$pass.A) / studies),
"\n B = slow passed ±20% criterion :",
sprintf("%.1f%%", 100 * sum(comp$pass.B) / studies),
"\n A = fast passed nonparametric CI:",
sprintf("%7.4f (empiric Type I Error)", sum(comp$pass.CL.A) / studies),
"\n B = slow passed nonparametric CI:",
sprintf("%7.4f (empiric Type I Error)", sum(comp$pass.CL.B) / studies),
"\n\n Significance limit of the binomial test =",
signif(binom.test(as.integer(alpha * studies), studies,
alternative = "less",
conf.level = 1 - alpha)$conf.int[2], 5), "\n")# Simulation settings
# 2,500 studies (24 subjects / arm)
# tmax (A = fast) : 0.8000 h (t½,a: 10.05 min)
# tmax (B = slow) : 1.2000 h (t½,a: 17.74 min)
# tmax (Reference): 1.0000 h (t½,a: 13.69 min)
#
# Simulation results
# A = fast
# Range : 0.1667 h, 3.5000 h
# Skewness: +0.7777
# B = slow
# Range : 0.3333 h, 6.0000 h
# Skewness: +0.7499
# Reference
# Range : 0.2500 h, 4.0000 h
# Skewness: +0.6738
#
# A = fast passed ±20% criterion : 57.9%
# B = slow passed ±20% criterion : 55.0%
# A = fast passed nonparametric CI: 0.0532 (empiric Type I Error)
# B = slow passed nonparametric CI: 0.0368 (empiric Type I Error)
#
# Significance limit of the binomial test = 0.057771Interesting, isn’t it? It confirms that the distributions of \(\small{\widetilde{t}_\text{max}}\) are
skewed to the right.32 33 With the ±20 % criterion both formulations
showed a passing-rate significantly larger than the expected 50 % (limit
51.7 %).
The empiric Type I Error of the nonparametric test is not significantly
above the nominal \(\small{\alpha=0.05}\).
If we follow the logic of the guidances,11 12 13 the limits based on \(\small{t_\text{max(R)}=1\,\text{h}}\) are \(\small{\{\theta_1,\theta_2\}=\{0.8\,\text{h},1.2\,\text{h}\}}\). Such limits would translate into a clincially relevant \(\small{\Delta}\) of only 12 minutes. I doubt whether that makes sense. What about a painkiller with \(\small{t_\text{max(R)}=30\,\text{min}}\)? Is a \(\small{\Delta}\) of six minutes clincially relevant? Which sampling interval would suffice to ‘catch’ \(\small{t_\text{max}}\) – two minutes?
Do we have a method to estimate the sample size of such a study? Nope. One could only perform simulations, which would require:
- Sufficient information about the PK of the drug and the formulations (absorption rate constant, eventual lag-time) allowing to set up a suitable model.
- Not only the PK parameters themselves but also their variability would be required. A published population PK would come handy.
- An assumed difference in tmax.
- Exploring different sampling schedules.
Good luck!
In a replicate design in 18 subjects (two administrations of the German 400 mg IR ibuprofen reference product three days apart) after the 1st administration the range of \(\small{t_\text{max}}\) was 0.25 – 4 hours (CV 94.3 %) and after the 2nd 0.5 – 2 hours (CV 62.3 %).37 It’s interesting that despite such a large variability \(\small{\widetilde{t}_\text{max}}\) differed only by two minutes. In my studies I observed a range of \(\small{t_\text{max}}\) of 0.5 – 4.5 hours (CV 50 %).
Say, we have sufficent information about the
PK as mentioned above, e.g., \(\small{t_{1/2}=1.93\,\text{h}}\), \(\small{t_\text{max(R)}=45\,\text{min}}\).
Let’s assume that the test is ten minutes faster than the reference.
Sampling every five minutes up to 1.5 hours (i.e., \(\small{2\times t_\text{max(R)}}\)), 1.75,
2, 2.25, 2.5, 3, 3.5, 4, 4.5, 5, 6, 8, and 12 hours. Parallel design and
we target power ≥ 80 %. In the
CI inclusion approach we
specify \(\small{\{\theta_1,\theta_2\}=\{\mp20\,\text{min}\}}\).
For \(\small{C_\text{max}}\) a
CVintra of 22.7 % and a CVinter
of 27.4 % was reported.37 With a total
(pooled) CV of 25.4 % in a parallel design assuming a T/R-ratio
of 0.95 we would need 56 subjects (80.4 % power) and for a T/R-ratio of
0.90 we would need 114 (80.1 % power) to demonstrate
BE for this metric.
# Due to the large sample size wilcox_test() is extremely slow
library(moments)
library(survival)
library(coin)
opt <- function(x, k10.d, tmax) {
# absorption rate constant for given elimination at tmax
log(x / k10.d) / (x - k10.d) - tmax
}
Ct <- function(D = D, F = F.d, V = V.d, k01 = k01.d, k10 = k10.d, t) {
# one-compartment model, no lag time
if (!isTRUE(all.equal(k01, k10))) {# common: k01 != k10
if (k10 > k01) {# absorption faster
C <- F * D * k01 / (V * (k01 - k10)) *
(exp(-k10 * t) - exp(-k01 * t))
}else { # elimination faster
C <- F * D * k10 / (V * (k10 - k01)) *
(exp(-k01 * t) - exp(-k10 * t))
}
}else { # flip-flop PK
k <- k10
C <- F * D / V * k * t * exp(-k * t)
}
return(C)
}
progr <- FALSE # in your own simulations set to TRUE
alpha <- 0.05 # level of the test
# ibuprofen
tmax <- setNames(c(0.75, 0.75 - 10 / 60), c("R", "T"))
studies <- 2500 # number of simulated studies
n <- 28 # number of subjects in each arm of a study
delta <- c(-20, +20) # acceptable differences (%)
# limits for median (T) - median (R)
limit <- signif((100 + delta) / 100, 9)
# limits for the CI inclusion approach (±20 minutes in hours)
theta1 <- signif(-20 / 60, 9)
theta2 <- signif(+20 / 60, 9)
D <- 400e3 # dose (µg)
# Index ".d" denotes theoretical value, ".c" its CV
F.d <- 0.9 # fraction absorbed
F.l <- 0.8 # lower limit
F.u <- 1 # upper limit
V.d <- 500 # volume of distribution (mL)
V.c <- 0.25 # CV 25% (lognormal)
k10.d <- log(2) / 1.93 # elimination rate constant (geom. mean of the paper)
k10.c <- 0.30 # CV 30% (lognormal)
# absorption rate constant
k01.dR <- uniroot(opt, interval = c(0, 24), tol = 1e-8,
k10.d = k10.d, tmax = tmax[["R"]])$root
k01.dT <- uniroot(opt, interval = c(0, 24), tol = 1e-8,
k10.d = k10.d, tmax = tmax[["T"]])$root
k01.c <- 0.35 # CV 35% (lognormal)
AErr <- 0.05 # analytical error CV 5% (normal)
LLOQ.f <- 0.05 # fraction of theoretical Cmax
Cmax.R <- Ct(D, F.d, V.d, k01.dR, k10.d, tmax[["R"]]) # µg/mL
LLOQ <- LLOQ.f * Cmax.R
t <- sort(unique(c(seq(0, 2 * tmax[["R"]], 5 / 60),
2.25, 2.5, 3, 3.5, 4, 4.5, 5, 6, 8, 12)))
R <- T <- data.frame(study = rep(1:studies, each = n * length(t)),
subject = rep(1:n, each = length(t)), t = t,
C = NA_real_)
res.R <- res.T <- data.frame(study = rep(1:studies, each = n),
subject = rep(1:n, studies), tmax = NA_real_)
comp <- data.frame(study = 1:studies, median.R = NA_real_, median.T = NA_real_,
ratio = NA_real_, pass = FALSE, pass.CL = FALSE)
set.seed(123456) # for reproducibility
if (progr) pb <- txtProgressBar(0, 1, 0, width = NA, style = 3)
for (study in 1:studies) {# subject’s PK parameters & profiles
F <- runif(n = n, min = F.l, max = F.u)
V <- rlnorm(n = n, meanlog = log(V.d) - 0.5 * log(V.c^2 + 1),
sdlog = sqrt(log(V.c^2 + 1)))
k01.Rs <- rlnorm(n = n, meanlog = log(k01.dR) - 0.5 * log(k01.c^2 + 1),
sdlog = sqrt(log(k01.c^2 + 1)))
k01.Ts <- rlnorm(n = n, meanlog = log(k01.dT) - 0.5 * log(k01.c^2 + 1),
sdlog = sqrt(log(k01.c^2 + 1)))
k10s <- rlnorm(n = n, meanlog = log(k10.d) - 0.5 * log(k10.c^2 + 1),
sdlog = sqrt(log(k10.c^2 + 1)))
for (subject in 1:n) {
C.R <- Ct(D, F = F[subject], V = V[subject],
k01 = k01.Rs[subject], k10 = k10s[subject], t)
C.T <- Ct(D, F = F[subject], V = V[subject],
k01 = k01.Ts[subject], k10 = k10s[subject], t)
# add analytical error (normal)
C.R <- C.R + rnorm(n = length(t), mean = 0, sd = abs(C.R * AErr))
C.T <- C.T + rnorm(n = length(t), mean = 0, sd = abs(C.T * AErr))
# assign NAs to Cs below LLOQ
C.R[C.R < LLOQ] <- NA
C.T[C.T < LLOQ] <- NA
# set NAs before tmax to zero
tmax.R <- t[which(C.R == max(C.R, na.rm = TRUE))]
tmax.T <- t[which(C.T == max(C.T, na.rm = TRUE))]
C.R[which(t[which(is.na(C.R))] < tmax.R)] <- 0
C.T[which(t[which(is.na(C.T))] < tmax.T)] <- 0
R$C[R$study == study & R$subject == subject] <- C.R
T$C[T$study == study & T$subject == subject] <- C.T
res.R$tmax[res.R$study == study & res.R$subject == subject] <- tmax.R
res.T$tmax[res.T$study == study & res.T$subject == subject] <- tmax.T
}
comp$median.R[study] <- median(res.R$tmax[res.R$study == study], na.rm = TRUE)
comp$median.T[study] <- median(res.T$tmax[res.T$study == study], na.rm = TRUE)
comp$ratio[study] <- comp$median.T[study] / comp$median.R[study]
if (comp$ratio[study] >= limit[1] & comp$ratio[study] <= limit[2])
comp$pass[study] <- TRUE
# 90% confidence interval of the Wilcoxon-Mann-Whitney test
tmax.TR <- data.frame(tmax = c(res.T$tmax[res.T$study == study],
res.R$tmax[res.R$study == study]),
treatment = factor(rep(c("T", "R"),
c(n, n))))
CI.TR <- signif(as.numeric(unlist(
confint(wilcox_test(tmax ~ rev(treatment),
data = tmax.TR,
distribution = "exact",
conf.int = TRUE,
conf.level = 1 - 2 * alpha))[1])), 9)
if (CI.TR[1] >= theta1 & CI.TR[2] <= theta2) comp$pass.CL[study] <- TRUE
if (progr) setTxtProgressBar(pb, study / studies)
} # patience please...
if (progr) close(pb)
cat("Simulation settings",
paste0("\n ", formatC(studies, format = "d", big.mark = ","),
" studies (", n, " subjects / arm)"),
"\n tmax (Test) :", sprintf("%.4f h", tmax[["T"]]),
sprintf("(t½,a: %.2f min)", 60 * log(2) / k01.dT),
"\n tmax (Reference):", sprintf("%.4f h", tmax[["R"]]),
sprintf("(t½,a: %.2f min)", 60 * log(2) / k01.dR),
"\n\nSimulation results",
"\n Test",
paste0("\n Range : ",
paste(sprintf("%.4f",
range(res.T$tmax, na.rm = TRUE)), collapse = " h, "), " h"),
paste0("\n Skewness: ", sprintf("%+.4f", skewness(res.T$tmax))),
"\n Reference",
paste0("\n Range : ",
paste(sprintf("%.4f",
range(res.R$tmax, na.rm = TRUE)), collapse = " h, "), " h"),
paste0("\n Skewness: ", sprintf("%+.4f", skewness(res.R$tmax))),
"\n\n Passed ±20% criterion :",
sprintf("%5.1f%%", 100 * sum(comp$pass) / studies),
"\n Passed nonparametric CI:",
sprintf("%5.1f%% (empiric power)", 100 * sum(comp$pass.CL) / studies), "\n")# Simulation settings
# 2,500 studies (28 subjects / arm)
# tmax (Test) : 0.5833 h (t½,a: 8.65 min)
# tmax (Reference): 0.7500 h (t½,a: 12.50 min)
#
# Simulation results
# Test
# Range : 0.1667 h, 2.2500 h
# Skewness: +0.7020
# Reference
# Range : 0.1667 h, 2.5000 h
# Skewness: +0.4922
#
# Passed ±20% criterion : 52.0%
# Passed nonparametric CI: 94.1% (empiric power)Seemingly the ±20 % criterion is pretty rigid. The ten minutes faster test product (\(\small{t_\text{max}=35\,\text{min}}\)) is already slightly below the lower border (\(\small{0.8\times t_\text{max(R)}=36\,\text{min}}\)). With this sample size the test product must not be more than seven minutes faster in order to achieve ≈80 % power.
On the other hand, we fare extremely well with the CI inclusion approach. However, with a more restrictive \(\small{\Delta=15\,\text{min}}\) we achieve only 60.5 % power. To achieve the desired power we would have to increase the sample size accordingly – regrettably by trial and error.
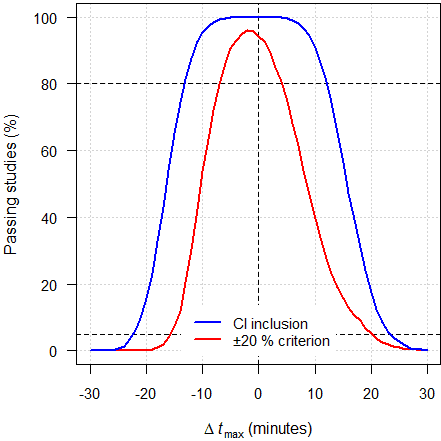
As expected, the power curve of the
CI inclusion approach is –
almost – symmetrical around zero.
The power curve of the ±20 % criterion is asymmetrical: Its maximum is
slightly shifted to the left and for and given \(\small{\Delta\,t_\text{max}}\) a negative
value has higher power than a negative one. That means, a faster test is
more likely to pass than a slower one. If, say, \(\small{\Delta\,t_\text{max}=-5\,\text{min}}\),
90.5 % of studies will pass but if \(\small{\Delta\,t_\text{max}=+5\,\text{min}}\)
only 74.8 %. This behavior is due to calculating a ratio while keeping
symmetrical limits. That’s flawed as if we would have kept back in the
day the BE limits at 80 – 120 % (see
this article).
Keep in mind that simulations depend on many assumptions about the PK of both formulations. Even if parameters of the reference product’s PK model are in the public domain, their variances are not necessarily.
If you have data of a previous study, Monte Carlo simulations may
help.
One of my studies: 600 mg IR
ibuprofen, fasting state, 2×2×2 crossover, 16 subjects (powered to
≥ 90 % for \(\small{C_\text{max}}\)),
sampling every 15 minutes up to 2.5 hours. Resampled \(\small{t_\text{max}}\) of the reference in
10^5 simulations.
library(moments)
sum.simple <- function(x, digits = 5) {
# Nonparametric summary:
# Remove Mean but keep eventual NAs
y <- summary(x, digits = digits)
if (nrow(y) == 6) {
y <- y[c(1:3, 5:6), ]
}else {
y <- y[c(1:3, 5:7), ]
}
return(y)
}
progr <- FALSE # in your own simulations set to TRUE
nsims <- 1e5L # Number of simulations
tmax <- c(1.25, 2.00, 1.00, 1.25, 2.50, 1.25, 1.50, 2.25,
1.00, 1.25, 1.50, 1.25, 2.25, 1.75, 2.50, 2.25)
aggr <- data.frame(sim = 1L:nsims,
R1 = NA_real_,
R2 = NA_real_,
pct.med.diff = NA_real_,
pass = FALSE)
n <- as.integer(length(tmax))
pct.delta <- 20 # Acc. to the guidance(s)
if (progr) pb <- txtProgressBar(0, 1, 0, width = NA, style = 3)
set.seed(123456) # for reproducibility
for (i in 1L:nsims) {
# Now we resample the distribution, call it R1 and R2
R1 <- sample(tmax, size = n, replace = TRUE)
R2 <- sample(tmax, size = n, replace = TRUE)
aggr[i, 2] <- median(R1)
aggr[i, 3] <- median(R2)
# arbitrary: Compare R2 with R1
aggr[i, 4] <- 100 * (aggr$R2[i] - aggr$R1[i]) / aggr$R1[i]
# Check whether medians differ by more than 20%
if (abs(aggr[i, 4]) <= pct.delta) aggr$pass[i] <- TRUE
if (progr) setTxtProgressBar(pb, i / nsims)
} # patience, please...
skew <- sprintf("%+.4f", skewness(aggr$pct.med.diff))
xlim <- c(-1, +1) * max(abs(range(c(-pct.delta, pct.delta,
aggr$pct.med.diff))))
if (progr) close(pb)
dev.new(width = 4.6, height = 4.6)
op <- par(no.readonly = TRUE)
par(mar = c(4, 4, 0, 0), cex.axis = 0.9)
hist(aggr[, 4], freq = FALSE, main = "", axes = FALSE, col = "lightblue1",
xlab = expression(italic(t)[max] * ": " *
tilde(R)[2] / tilde(R)[1] * " (%)"),
ylab = "Density")
abline(v = c(-pct.delta, pct.delta), lty = 1, col = "red")
abline(v = quantile(aggr[, 4], probs = c(0.025, 0.5, 0.975)),
col = "black", lty = 2)
axis(1, at = seq(xlim[1], xlim[2], pct.delta))
axis(2, las = 1)
legend("topright", bg = "white", box.lty = 0, cex = 0.9,
legend = bquote(skewness == .(skew)), x.intersp = 0)
par(op)
txt <- paste0("\nNot equivalent if medians differ by more than 20%",
sprintf("\nEmpiric power = %.2f%%",
100 * (1 - sum(aggr$pass == FALSE) / nsims)), "\n\n")
res <- sum.simple(aggr[c(2, 3:5)], digits = 4)
dimnames(res)[[2]][3:4] <- c("diff. med. (%)", " passed")
print(res)
cat(txt)# R1 R2 diff. med. (%) passed
# Min. :1.000 Min. :1.000 Min. :-50.000 Mode :logical
# 1st Qu.:1.375 1st Qu.:1.375 1st Qu.:-15.385 FALSE:34887
# Median :1.500 Median :1.500 Median : 0.000 TRUE :65113
# 3rd Qu.:1.750 3rd Qu.:1.750 3rd Qu.: 18.182
# Max. :2.500 Max. :2.500 Max. :100.000
#
# Not equivalent if medians differ by more than 20%
# Empiric power = 65.11%
dashed black lines 2.5 percentile, median, 97.5 percentile.
Shocking, isn’t it? With the ±20 % criterion we have only ≈ 65 % power to show that the reference is equivalent to itself.
Good luck if your product differs from the reference. Now I used the same data but shifted a ‘test’ product by eight minutes (–10.7 % of the reference’s \(\small{t_\text{max}}\)). Theoretically that would mean 1.12 hours, but we round it to the closest multiple of the sampling schedule’s 15 minutes.
library(moments)
roundClosest <- function(x, y) {
# Round x to the closest multiple of y
return(y * round(x / y))
}
sum.simple <- function(x, digits = 5) {
# Nonparametric summary:
# Remove Mean but keep eventual NAs
y <- summary(x, digits = digits)
if (nrow(y) == 6) {
y <- y[c(1:3, 5:6), ]
}else {
y <- y[c(1:3, 5:7), ]
}
return(y)
}
tmax <- c(1.25, 2.00, 1.00, 1.25, 2.50, 1.25, 1.50, 2.25,
1.00, 1.25, 1.50, 1.25, 2.25, 1.75, 2.50, 2.25)
sampling <- 15/60 # Sampling interval
progr <- FALSE # in your own simulations set to TRUE
nsims <- 1e5L # Number of simulations
aggr <- data.frame(sim = 1L:nsims,
R = NA_real_,
T = NA_real_,
pct.med.diff = NA_real_,
pass = FALSE)
n <- as.integer(length(tmax))
pct.delta <- 20 # Acc. to the guidance(s)
if (progr) pb <- txtProgressBar(0, 1, 0, width = NA, style = 3)
set.seed(123456) # for reproducibility
for (i in 1L:nsims) {
# Now we resample the distribution, call it R and T
R <- sample(tmax, size = n, replace = TRUE)
T <- sample(tmax, size = n, replace = TRUE)
# Eight minutes earlier, round to the closest 15 minutes
T <- roundClosest(T - 8 / 60, sampling)
aggr[i, 2] <- median(R)
aggr[i, 3] <- median(T)
# Compare T with R
aggr[i, 4] <- 100 * (aggr$T[i] - aggr$R[i]) / aggr$R[i]
# Check whether medians differ by more than 20%
if (abs(aggr[i, 4]) <= pct.delta) aggr$pass[i] <- TRUE
if (progr) setTxtProgressBar(pb, i / nsims)
} # patience, please...
skew <- sprintf("%+.4f", skewness(aggr$pct.med.diff))
xlim <- c(-1, +1) * max(abs(range(c(-pct.delta, pct.delta,
aggr$pct.med.diff))))
if (progr) close(pb)
dev.new(width = 4.6, height = 4.6)
op <- par(no.readonly = TRUE)
par(mar = c(4, 4, 0, 0), cex.axis = 0.9)
hist(aggr[, 4], freq = FALSE, main = "", axes = FALSE, col = "lightblue1",
xlab = expression(italic(t)[max] * ": " *
tilde(T) / tilde(R) * " (%)"),
ylab = "Density")
abline(v = c(-pct.delta, pct.delta), lty = 1, col = "red")
abline(v = quantile(aggr[, 4], probs = c(0.025, 0.5, 0.975)),
col = "black", lty = 2)
axis(1, at = seq(xlim[1], xlim[2], pct.delta))
axis(2, las = 1)
legend("topright", bg = "white", box.lty = 0, cex = 0.9,
legend = bquote(skewness == .(skew)), x.intersp = 0)
par(op)
txt <- paste0("\nNot equivalent if medians differ by more than 20%",
sprintf("\nEmpiric power = %.2f%%",
100 * (1 - sum(aggr$pass == FALSE) / nsims)), "\n\n")
res <- sum.simple(aggr[c(2, 3:5)], digits = 4)
dimnames(res)[[2]][3:4] <- c("diff. med. (%)", " passed")
print(res)
cat(txt)# R T diff. med. (%) passed
# Min. :1.000 Min. :0.750 Min. :-61.11 Mode :logical
# 1st Qu.:1.375 1st Qu.:1.125 1st Qu.:-30.77 FALSE:48403
# Median :1.500 Median :1.250 Median :-16.67 TRUE :51597
# 3rd Qu.:1.750 3rd Qu.:1.500 3rd Qu.: 0.00
# Max. :2.500 Max. :2.250 Max. : 80.00
#
# Not equivalent if medians differ by more than 20%
# Empiric power = 51.60%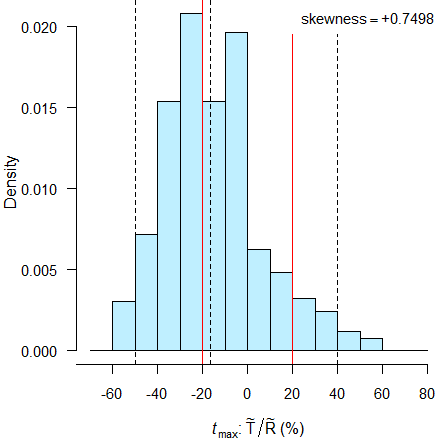
dashed black lines 2.5 percentile, median, 97.5 percentile.
 ©
CC-BY-SA 2.0 ICMA Photos
©
CC-BY-SA 2.0 ICMA Photos
Just not realistic to demonstrate BE. ~52% power is hardly better than tossing a coin…
We would need approximately one hundred subjects for ≈ 80 % power. Recall than in the original study we achieved 90 % power with 16 subjects.
Next I tried the reference data.37 Since the sampling schedule was insufficient, I fitted a one-compartment model and performed NCA with sampling every five minutes. Recall that in this study the reference was administered twice.
I compared \(\small{t_\text{max}}\) of the second period with the one of the first.
library(moments)
roundClosest <- function(x, y) {
# Round x to the closest multiple of y
return(y * round(x / y))
}
sum.simple <- function(x, digits = 5) {
# Nonparametric summary:
# Remove Mean but keep eventual NAs
y <- summary(x, digits = digits)
if (nrow(y) == 6) {
y <- y[c(1:3, 5:6), ]
}else {
y <- y[c(1:3, 5:7), ]
}
return(y)
}
############################################################
# Wagener and Vögtle-Junkert (1996). One-compartment model #
# and fitted concentrations with five minutes sampling #
############################################################
tmax.p1 <- c(60, 50, 30, 85, 25, 80, 55, 5, 30,
65, 165, 50, 130, 30, 30, 45, 55, 50) / 60
tmax.p2 <- c(30, 105, 100, 110, 40, 30, 130, 55, 40,
45, 40, 35, 70, 85, 30, 90, 25, 35) / 60
progr <- FALSE # in your own simulations set to TRUE
nsims <- 1e5L # Number of simulations
aggr <- data.frame(sim = 1L:nsims,
R.p1 = NA_real_,
R.p2 = NA_real_,
pct.med.diff = NA_real_,
pass = FALSE)
n <- as.integer(length(tmax.p1))
pct.delta <- 20 # Acc. to the guidance(s)
if (progr) pb <- txtProgressBar(0, 1, 0, width = NA, style = 3)
set.seed(123456) # for reproducibility
for (i in 1L:nsims) {
# Now we resample the distribution, call it R1 and R2
R.p1 <- sample(tmax.p1, size = n, replace = TRUE)
R.p2 <- sample(tmax.p2, size = n, replace = TRUE)
aggr[i, 2] <- median(R.p1)
aggr[i, 3] <- median(R.p2)
# Compare R in period 2 with R in period 1
aggr[i, 4] <- 100 * (aggr$R.p2[i] - aggr$R.p1[i]) / aggr$R.p1[i]
# Check whether medians differ by more than 20%
if (abs(aggr[i, 4]) <= pct.delta) aggr$pass[i] <- TRUE
if (progr) setTxtProgressBar(pb, i / nsims)
} # patience, please...
skew <- sprintf("%+.4f", skewness(aggr$pct.med.diff))
xlim <- c(-1, +1) * max(abs(range(c(-pct.delta, pct.delta,
aggr$pct.med.diff))))
if (progr) close(pb)
dev.new(width = 4.6, height = 4.6)
op <- par(no.readonly = TRUE)
par(mar = c(4, 4, 0, 0), cex.axis = 0.9)
hist(aggr[, 4], freq = FALSE, main = "", axes = FALSE, col = "lightblue1",
xlab = expression(italic(t)[max] * ": " *
tilde(R)[p2] / tilde(R)[p1] * " (%)"),
ylab = "Density")
abline(v = c(-pct.delta, pct.delta), lty = 1, col = "red")
abline(v = quantile(aggr[, 4], probs = c(0.025, 0.5, 0.975)),
col = "black", lty = 2)
axis(1, at = seq(xlim[1], xlim[2], pct.delta),
labels = signif(seq(xlim[1], xlim[2], pct.delta), 2))
axis(2, las = 1)
legend("topright", bg = "white", box.lty = 0, cex = 0.9,
legend = bquote(skewness == .(skew)), x.intersp = 0)
par(op)
txt <- paste0("\nNot equivalent if medians differ by more than 20%",
sprintf("\nEmpiric power = %.2f%%",
100 * (1 - sum(aggr$pass == FALSE) / nsims)), "\n\n")
res <- sum.simple(aggr[c(2, 3:5)], digits = 4)
dimnames(res)[[2]][3:4] <- c("diff. med. (%)", " passed")
print(res)
cat(txt)# R.p1 R.p2 diff. med. (%) passed
# Min. :0.4583 Min. :0.5000 Min. :-69.231 Mode :logical
# 1st Qu.:0.8333 1st Qu.:0.6667 1st Qu.:-21.053 FALSE:58247
# Median :0.8333 Median :0.7083 Median :-11.111 TRUE :41753
# 3rd Qu.:0.8750 3rd Qu.:0.9167 3rd Qu.: 13.636
# Max. :2.1667 Max. :1.7917 Max. :233.333
#
# Not equivalent if medians differ by more than 20%
# Empiric power = 41.75%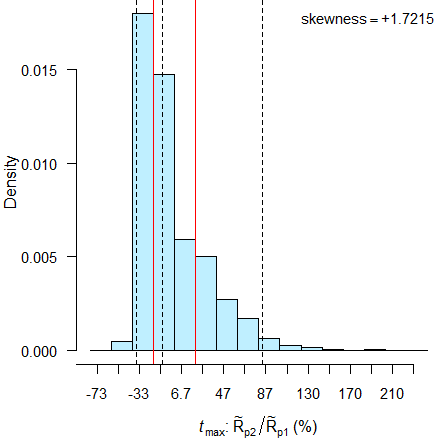
dashed black lines 2.5 percentile, median, 97.5 percentile.
The distribution is extremely skewed (≈ +1.72). Contrary to identical medians of 45 minutes37 (due to to the wide sampling intervals), we find medians of 50 minutes in the first period and 42.5 minutes in the second. Therefore, assessment by the ±20 % criterion is a complete disaster. ***
top of section ↩︎ previous section ↩︎
Remarks
Sensitivity and Bias of tmax
\(\small{t_\text{max}}\) and \(\small{C_\text{max}}\) are not sensitive to even substantial changes in the rate of absorption \(\small{k_{01}}\), since both are composite pharmacokinetic metrics.32 In a one compartment model they depending on \(\small{k_{01}}\) and the elimination rate constant \(\small{k_{10}}\).38 Whereas the former is a property of the formulation – we are interested in – the latter is a property of the drug. \[\eqalign{ t_\textrm{max}&=\frac{\log_{e}(k_{01}/k_{10})}{k_{01}-k_{10}}\\ C_\textrm{max}&=\frac{f\cdot D\cdot k_{01}}{V\cdot (k_{01}-k_{10})}\large(\small\exp(-k_{10}\cdot t_\textrm{max})-\exp(-k_{01}\cdot t_\textrm{max})\large)\tag{3}}\]
Especially \(\small{t_\text{max}}\) is a poor predictor of differences in the rate of absorption.
Example: An IR formulation, one compartment model with complete absorption. \(\small{D=100}\), \(\small{V=3}\), absorption half lives 30 minutes (Reference) and 21 minutes (Test), elimination half life four hours. Sigmoid effect model identical for both formulations: \(\small{E_\textrm{max}=125}\), \(\small{EC_{50}=50}\), \(\small{\gamma=0.5}\).
C.fun <- function(D, f, V, k01, k10, t) {
# PK (one compartment model)
C <- D * f * k01 / (V * (k01 - k10)) * (exp(-k10 * t) - exp(-k01 * t))
tmax <- log(k01 / k10) / (k01 - k10)
Cmax <- f * D * k01 / (V * (k01 - k10)) *
(exp(-k10 * tmax) - exp(-k01 * tmax))
AUC <- f * D / V / k10
res <- list(C = C, Cmax = Cmax, tmax = tmax, AUC = AUC)
return(res)
}
E.fun <- function(Emax, EC50, gamma, x) {
# PD (sigmoidal link model)
Ef <- (Emax * x^gamma)/(x^gamma + EC50^gamma)
return(Ef)
}
NCA <- function(t, C) {
x <- data.frame(t = t, C = C, pAUC = 0)
for (i in 1:(nrow(x) - 1)) {
if (x$C[i+1] < x$C[i]) {
x$pAUC[i+1] <- (x$t[i+1] - x$t[i]) * (x$C[i+1] - x$C[i]) /
log(x$C[i+1] / x$C[i])
}else {
x$pAUC[i+1] <- 0.5 * (x$t[i+1] - x$t[i]) *
(x$C[i+1] + x$C[i])
}
}
Cmax <- max(C)
tmax <- t[C == Cmax]
AUClast <- tail(cumsum(x$pAUC), 1)
x <- tail(x[, 1:2], 3)
m <- lm(log(C) ~ t, data = x)
lambda.z <- -coef(m)[[2]]
AUCinf <- AUClast + tail(x$C, 1) / lambda.z
res <- list(Cmax = Cmax, tmax = tmax,
AUClast = AUClast, AUCinf = AUCinf)
return(res)
}
D <- 100
V <- 3
f <- 1
k01.R <- log(2) / (30 / 60)
k01.T <- log(2) / (21 / 60)
k10 <- log(2) / 4
Emax <- 125
EC50 <- 50
gamma <- 0.5
t <- seq(0, 24, length.out = 1001)
smpl <- c(seq(0, 100, 10), 120, 135, 150, 180,
210, 240, 360, 540, 720, 960, 1440) / 60
tmp <- C.fun(D, f, V, k01.R, k10, t)
C.R <- tmp$C
AUC.R <- tmp$AUC
Cmax.R <- tmp$Cmax
tmax.R <- tmp$tmax
tmp <- C.fun(D, f, V, k01.T, k10, t)
C.T <- tmp$C
AUC.T <- tmp$AUC
Cmax.T <- tmp$Cmax
tmax.T <- tmp$tmax
E.R <- E.fun(Emax, EC50, gamma, C.R)
E.T <- E.fun(Emax, EC50, gamma, C.T)
Emax.R <- optimize(E.fun, interval = range(C.R), maximum = TRUE,
Emax = Emax, EC50 = EC50, gamma = gamma)$objective
Emax.T <- optimize(E.fun, interval = range(C.T), maximum = TRUE,
Emax = Emax, EC50 = EC50, gamma = gamma)$objective
res <- data.frame(AUC = c(AUC.R, AUC.T, AUC.T/AUC.R, NA),
Cmax = c(Cmax.R, Cmax.T, Cmax.T / Cmax.R, NA),
tmax = c(tmax.R, tmax.T, tmax.T / tmax.R, tmax.T - tmax.R),
Emax = c(Emax.R, Emax.T, Emax.T / Emax.R, NA),
t.Emax = c(t[E.R == max(E.R)], t[E.T == max(E.T)], NA,
t[E.T == max(E.T)] - t[E.R == max(E.R)]))
obs.R <- C.fun(D, f, V, k01.R, k10, smpl)$C
obs.T <- C.fun(D, f, V, k01.T, k10, smpl)$C
NCA.R <- NCA(smpl, obs.R)
NCA.T <- NCA(smpl, obs.T)
obs <- data.frame(AUClast = c(NCA.R$AUClast, NCA.T$AUClast,
NCA.T$AUClast / NCA.R$AUClast, NA),
AUCinf = c(NCA.R$AUCinf, NCA.T$AUCinf,
NCA.T$AUCinf / NCA.R$AUCinf, NA),
Cmax = c(NCA.R$Cmax, NCA.T$Cmax,
NCA.T$Cmax / NCA.R$Cmax, NA), RE1 = NA,
tmax = c(NCA.R$tmax, NCA.T$tmax, NCA.T$tmax / NCA.R$tmax,
NCA.T$tmax - NCA.R$tmax), RE2 = NA)
obs$RE1 <- 100 * (obs$Cmax - res$Cmax) / res$Cmax
obs$RE2 <- 100 * (obs$tmax - res$tmax) / res$tmax
names(obs)[c(4, 6)] <- rep("% RE", 2)
row.names(obs) <- row.names(res) <- c(" R", " T", "T / R", "T - R")
dev.new(width = 4.5, height = 4.5, record = TRUE)
op <- par(no.readonly = TRUE)
invisible(split.screen(c(2, 1)))
screen(1)
par(mar = c(3, 2.9, 1.1, 0.4), cex.axis = 0.8,
xaxs = "i", yaxs = "i")
plot(t, C.R, type = "n", axes = FALSE,
ylim = 1.04*c(0, max(Cmax.T, Cmax.R)),
xlab = "", ylab = "")
axis(1, at = seq(0, 24, 4))
axis(2, las = 1)
mtext("concentration", 2, line = 2)
lines(t, C.R, lwd = 3, col = "#1010FF80")
lines(t, C.T, lwd = 3, col = "#FF101080")
legend("topright", legend = c("R", "T"),
col = c("#1010FF80", "#FF101080"),
box.lty = 0, cex = 0.8, lwd = 3)
box()
screen(2)
par(mar = c(4, 2.9, 0.1, 0.4), cex.axis = 0.8,
xaxs = "i", yaxs = "i")
plot(t, E.R, type = "n", axes = FALSE,
ylim = 1.04*c(0, max(E.R, E.T)),
xlab = "time", ylab = "")
axis(1, at = seq(0, 24, 4))
axis(2, las = 1)
mtext("effect", 2, line = 2)
lines(t, E.R, lwd = 3, col = "#1010FF80")
lines(t, E.T, lwd = 3, col = "#FF101080")
legend("topright", legend = c("R", "T"),
col = c("#1010FF80", "#FF101080"),
box.lty = 0, cex = 0.8, lwd = 3)
box()
close.screen(all.screens = TRUE)
par(op)
print(round(res, 4))# AUC Cmax tmax Emax t.Emax
# R 192.3593 24.7666 1.7143 51.6343 1.704
# T 192.3593 26.3893 1.3481 52.5986 1.344
# T / R 1.0000 1.0655 0.7864 1.0187 NA
# T - R NA NA -0.3662 NA -0.360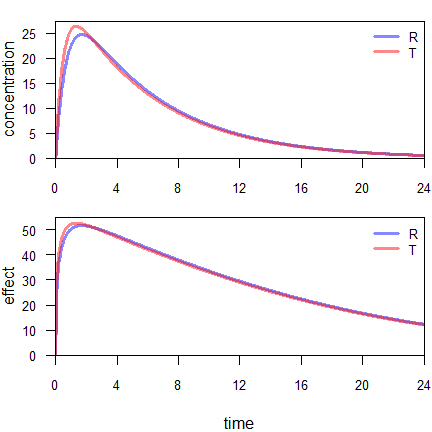
Fig. 10 Concentration and linked effect.
Although absorption of the Test is 30 % faster than the one of the Reference, its \(\small{t_\text{max}}\) occurs only ≈21 minutes earlier. The T/R-ratio of \(\small{C_\text{max}}\) is 106.6 %. Of course, the \(\small{AUC\text{s}}\) are identical.
It’s a common misconception that safety is directly related
to \(\small{C_\text{max}}\). Linking to
the effect site dampens the peaks. Hence, the T/R-ratio of \(\small{E_\text{max}}\) is only 101.9 %.39 The
maximum effect of the Test occurs ≈22 minutes earlier than the one of
the Reference.
As an aside, \(\small{E_\text{max}}\)
occurs commonly earlier than \(\small{C_\text{max}}\).
What do we obtain by NCA with rich sampling (every ten minutes till two hours, 2.25, 2.5, 3, 3.5, 4, 6, 9, 12, 16, and 24 hours)?
# AUClast AUCinf Cmax % RE tmax % RE
# R 188.7237 192.1587 24.7597 -0.0279 1.6667 -2.7778
# T 188.8800 192.1739 26.3883 -0.0038 1.3333 -1.0921
# T / R 1.0008 1.0001 1.0658 0.0242 0.8000 1.7338
# T - R NA NA NA NA -0.3333 -8.9826We see a practically negligible bias of \(\small{C_\text{max}}\) – though it would be larger with wider sampling intervals – and a substantial one of \(\small{t_\text{max}}\), since we are never able to ‘catch’ the true values. The observed \(\small{C_\text{max}}\) is always lower than the true one because with any given schedule we will sample either before or after the true \(\small{t_\text{max}}\).
If we follow the recent draft product-specific guidances,11 12 13 it will be a close shave (tmax –20%).
Comparison of Medians?
Nonparametric analysis is the appropriate approach for estimating the discretely recorded \(\small{t_\text{max}}\).31 40 41
It is a misconception that the Wilcoxon
signed-rank test and the Mann–Whitney
U test compare medians. The Wilcoxon signed-rank test (for
paired samples) employs the Hodges-Lehmann
estimator. The Mann–Whitney U test (for independent
samples) compares the median of the difference between a sample
from \(\small{x}\) and a sample
from \(\small{y}\).
Both are unbiased estimators of a shift in location only if
distributions are identical (though not necessarily symmetrical).
However, in well-controlled studies (e.g., in
BE) this is likely the case.41 See also the simulations above, where the skewness of products’ \(\small{\widetilde{t}_\text{max}}\) was
similar. Recall that in parametric methods independent
and identical distributions are assumed as well.
Due to the discrete nature of the underlying distribution, the ≈90 %
confidence interval is always apparently wider than the 90 %
CI based on the normal
distribution. However, such a comparison is not fair, since the
distribution is not normal.
Below the exact confidence levels in balanced and slightly imbalanced 2×2×2 crossover designs.
# Distribution of the Wilcoxon signed-rank (aka rank sum) Statistic
nvec <- function(n) {
ni <- trunc(n / 2)
nv <- rep.int(ni, times = 2)
r <- n - 2 * ni
if(!r == 0) nv <- nv + c(rep.int(1, r), rep.int(0, 2 - r))
return(as.integer(nv))
}
alpha <- 0.05 # for desired ~90% CI
n <- 12L:120L
res <- data.frame(N = n, m = NA_integer_, n = NA_integer_)
for (i in seq_along(n)) {
res[i, 2:3] <- nvec(n[i])
# quantile function
k <- qwilcox(p = alpha,
m = res$m[i], n = res$n[i])
if (k == 0) k <- k + 1
# distribution function
res$conf.level[i] <- 1 - 2 * pwilcox(q = k - 1,
m = res$m[i], n = res$n[i])
}
print(res, row.names = FALSE)# N m n conf.level
# 12 6 6 0.9069264
# 13 7 6 0.9265734
# 14 7 7 0.9026807
# 15 8 7 0.9061383
# 16 8 8 0.9170163
# 17 9 8 0.9072810
# 18 9 9 0.9060880
# 19 10 9 0.9052805
# 20 10 10 0.9107904
# 21 11 10 0.9013824
# 22 11 11 0.9120539
# 23 12 11 0.9091576
# 24 12 12 0.9112662
# 25 13 12 0.9023576
# 26 13 13 0.9091527
# 27 14 13 0.9055210
# 28 14 14 0.9061319
# 29 15 14 0.9067843
# 30 15 15 0.9024742
# 31 16 15 0.9067410
# 32 16 16 0.9061876
# 33 17 16 0.9057654
# 34 17 17 0.9013126
# 35 18 17 0.9041047
# 36 18 18 0.9029409
# 37 19 18 0.9019280
# 38 19 19 0.9035907
# 39 20 19 0.9051653
# 40 20 20 0.9035004
# 41 21 20 0.9019906
# 42 21 21 0.9028384
# 43 22 21 0.9036705
# 44 22 22 0.9017265
# 45 23 22 0.9046107
# 46 23 23 0.9002555
# 47 24 23 0.9006013
# 48 24 24 0.9027958
# 49 25 24 0.9007585
# 50 25 25 0.9006068
# 51 26 25 0.9004985
# 52 26 26 0.9020722
# 53 27 26 0.9035707
# 54 27 27 0.9030133
# 55 28 27 0.9025131
# 56 28 28 0.9001460
# 57 29 28 0.9012392
# 58 29 29 0.9004810
# 59 30 29 0.9029184
# 60 30 30 0.9004952
# 61 31 30 0.9011928
# 62 31 31 0.9002387
# 63 32 31 0.9021996
# 64 32 32 0.9025308
# 65 33 32 0.9001599
# 66 33 33 0.9017373
# 67 34 33 0.9006684
# 68 34 34 0.9007852
# 69 35 34 0.9009153
# 70 35 35 0.9021280
# 71 36 35 0.9009372
# 72 36 36 0.9008405
# 73 37 36 0.9007642
# 74 37 37 0.9016981
# 75 38 37 0.9004213
# 76 38 38 0.9001633
# 77 39 38 0.9020363
# 78 39 39 0.9006456
# 79 40 39 0.9013446
# 80 40 40 0.9009302
# 81 41 40 0.9005431
# 82 41 41 0.9010410
# 83 42 41 0.9015318
# 84 42 42 0.9009986
# 85 43 42 0.9004941
# 86 43 43 0.9008202
# 87 44 43 0.9011458
# 88 44 44 0.9005209
# 89 45 44 0.9016222
# 90 45 45 0.9001134
# 91 46 45 0.9003059
# 92 46 46 0.9012281
# 93 47 46 0.9005427
# 94 47 47 0.9005926
# 95 48 47 0.9006506
# 96 48 48 0.9013977
# 97 49 48 0.9006428
# 98 49 49 0.9005814
# 99 50 49 0.9005307
# 100 50 50 0.9011339
# 101 51 50 0.9003244
# 102 51 51 0.9001724
# 103 52 51 0.9000328
# 104 52 52 0.9005161
# 105 53 52 0.9009919
# 106 53 53 0.9007486
# 107 54 53 0.9005194
# 108 54 54 0.9008802
# 109 55 54 0.9012374
# 110 55 55 0.9009200
# 111 56 55 0.9006174
# 112 56 56 0.9008761
# 113 57 56 0.9011342
# 114 57 57 0.9007557
# 115 58 57 0.9003925
# 116 58 58 0.9005651
# 117 59 58 0.9007395
# 118 59 59 0.9003103
# 119 60 59 0.9009961
# 120 60 60 0.9010812Alternatives42 43 44 not requiring identical distributions are out of scope of this article.
Low Power?
Though stated in the WHO’s guideline,27 it is also a misconception that a statistical comparison of \(\small{t_\text{max}}\) with a nonparametric method has low power. For instance, the Wilcoxon signed-rank test (for paired differences) and the Mann–Whitney U test (for independent samples) have an asymptotical power of \(\small{3/\pi\approx95.5\%}\) for normal distributed data. For small sample sizes sufficient power was confirmed in simulations.45 Of course, if data don’t follow a normal distribution, nonparametric tests are more powerful than their parametric counterparts.
Rich sampling in the early part of the profile (\(\small{\leq 2\times t_\textrm{max}}\)) is generally recommended in order ‘catch’ \(\small{C_\text{max}}\). If one wants to follow the recent draft product-specific guidances,11 12 13 it might be necessary to aim at sampling intervals narrower than usual. Sample size estimation for this approach is not implemented in any software.
Alternatives to tmax?
An alternative to comparing \(\small{t_\text{max}}\) would be to assess the ‘early exposure’ (i.e., by a partial \(\small{AUC}\)) as recommended by the FDA46 and Health Canada47 for drugs with rapid onset of action.
However, this PK metric is
extremely variable and might require a replicate design in order to
apply reference-scaling (RSABE
or ABEL).
Note that reference-scaling for partial \(\small{AUC\textsf{s}}\) is acceptable for
the EMA.10
Health Canada requires for drugs with rapid onset of action the cut-off
time as the subject’s \(\small{t_\text{max}}\) of the reference,48 which
can be difficult to set up in some software packages. Similarly to the
comparison of \(\small{C_\text{max}}\),
only the point estimate has to lie within 80.0 – 125.0 % and hence, a
parallel or a simple 2×2×2 crossover design would be sufficient.
Interlude: FDA, Health Canada
Interesting is an older guidance of the FDA.
“An early exposure measure may be informative on the basis of appropriate clinical efficacy/safety trials and/or pharmacokinetic/pharmacodynamic studies that call for better control of drug absorption into the systemic circulation (e.g., to ensure rapid onset of an analgesic effect or to avoid an excessive hypotensive action of an antihypertensive). In this setting, the guidance recommends use of partial AUC as an early exposure measure. We recommend that the partial area be truncated at the population median of Tmax values for the reference formulation.
Sorry folks but the population [sic] median is unknown. Is the sample median meant? Or is it the value reported in the RLD’s label? What if – stupid enough – only the arithmetic mean is given?
In the latest guidance for NDAs or INDs we find:
“ […] for certain classes of drugs (e.g., analgesic drug products), an evaluation of the partial exposure could be scientifically appropriate to support the determination of the relative BA of the drug product. The FDA recommends the use of partial AUC as a partial exposure measure. The time to truncate the partial AUC should be related to a clinically relevant response measure. The sponsor should collect sufficient quantifiable samples to allow an adequate estimation of the partial AUC. Sponsors should consult the appropriate review division for questions on the suitability of the response measure or the use of partial exposure.
It makes sense to base cut-off times on pharmacodynamics, which is in line with guidances for multiphasic release products of the FDAand Health Canada, as well as with the recent draft guideline for IR products of the ICH.
“The partial AUCs, AUC0–1.5 and AUC1.5–t, have been determined to be the most appropriate parameters for evaluation of the drug bioavailability responsible for the sleep onset and sleep maintenance phases, respectively. […] These two partial AUCs will ensure that the pharmacokinetic profiles of test and reference products are sufficiently similar that there will be no significant difference in sleep onset, sleep maintenance, and lack of residual effects between the test and reference products. “The sampling time (T1) for the first pAUC is based on time at which 90–95% of subjects are likely to achieve optimal early onset of response. Because the rate of initial methylphenidate absorption is associated with the rate of early onset of response, the sampling time “T1” is determined based on Tmax of the immediate-release portion of the formulation. […] T2 is based on the school hours and […] T3 is based on the efficacy duration claim of Concerta® from the pivotal clinical studies. “The requirement for pAUC assessment metrics for multiphasic modified‐release formulations will be based on data available from various sources, including but not limited to peer‐reviewed scientific literature and the approved Canadian labelling, as applicable. The time course of changes in the rate of drug delivery throughout the day should be reconciled with generally accepted and clinically relevant response data generated from a well‐designed randomized clinical trial program. Specifically, standards based on the 90% confidence interval of pAUC metrics should be met. The specific pAUC time intervals to be considered will be based on clinical data showing the therapeutic relevance of the particular time interval (e.g. early onset, maintenance, dose clearance, fasted versus fed state). Selected time intervals should be justified, specified a priori and applied to all study subjects for both the test and reference products. “[…] in some situations, Cmax and AUC(0-t) may be insufficient to adequately assess the BE between two products, e.g., when the early onset of action is clinically relevant. In these cases, an additional PK parameter, such as area under the concentration vs. time curve between two specific time points (pAUC), may be applied. This pAUC is typically evaluated from the time of drug administration until a predetermined time point that is related to a clinically relevant pharmacodynamic measure. Samples should be spaced such that the pAUC can be estimated accurately.
For the EMA cut-off
time(s) should be based on pharmacokinetics.10 Nice on paper… Mean plots in the originator’s
approval package will be misleading. Even if the package contains
‘spaghetti plots’,54 55 it will be difficult to identify a
‘trough’ between release phases.
Furthermore, contrary to the
FDA and Health
Canada, partial \(\small{AUC\textsf{s}}\) are required
additionally to \(\small{t_\text{max}}\).
Conclusions
Recall that in the simple simulations we had perfectly matching products (the average PK-parameters were identical). If we apply an appropriate statistical method, we could confirm that (i.e., detected no differences in \(\small{t_\text{max}}\)).
There is no guarantee that by looking (‽) at reported medians / IQRs / ranges an assessor will arrive at the same conclusions as the applicant. A great deal of discussions on its way.
Assessing tmax based on eyeballing ‘apparent’ differences of medians, its ‘variability’ or range is bad science and thus, should be abandoned.
IMHO, the statement in the guidelines9 10»A [formal] statistical evaluation of tmax is not required«
does not preclude to perform one:
Only (‼) if clinically relevant, pre-specify an acceptance range for tmax and assess the ≈90% confidence interval by an appropriate nonparametric method.
I did so since the mid 1980s and – even after the EMA’s BE guideline9 of 2010 – never received a single deficiency letter in this respect.
Given the theoretical considerations,32 as well as my observations and simulations, at least a modified criterion \(\small{-20\%\leq\Delta\,\widehat{t}_\text{max}\leq25\%}\) could be considered as a quick – though doubtful – fix.
»Comparable median (≤ 20 % difference) and range for Tmax.«
is statistically questionable and should be challenged.
“Enlightenment is man’s release from his self-incurred tutelage. Tutelage is man’s inability to make use of his understanding without direction from another. Self-incurred is this tutelage when its cause lies not in lack of reason but in lack of resolution and courage to use it without direction from another. Sapere aude! “Have courage to use your own reason!” – that is the motto of enlightenment.
Unresolved
In order to ‘catch’ \(\small{t_\text{max}}\) in all subjects under all treatments, likely a much tighter sampling schedule than usual is required.
In the simulations we observed in the CI inclusion approach no significantly inflated Type I Error. However,
- the tight sampling ended too early. Hence, in some cases tmax was observed later than the true one.
- The Wilcoxon
signed-rank test (for paired differences) and the Mann–Whitney
U test give unbiased estimates of the shift in location
only if distributions are identical. Based on the skewness in
the simulations the distributions were only
similar.
Alternatives42 43 44 not requiring identical distributions are not trivial and computationally intensive. Furthermore, they give only a probability and no confidence interval. A less powerful method (requiring fewer assumptions) for paired samples is the sign test, provided in the functionsign_test()of packagecoin.2
For any approach sample size estimation is difficult and computationally demanding. Since it is currently not supported in software, you have to roll out your own code – relying on numerous assumptions.
top of section ↩︎ previous section ↩︎
Acknowledgment
Susana Almeida (IGBA), Jean-Michel Cardot, Jiří Hofmann (Zentiva), and members of the BEBA-Forum ElMaestro and Ohlbe for fruitful discussions.
Licenses
Helmut Schütz 2024
R, all packages, and
pandoc GPL 3.0,
klippy MIT.
1st version April 19, 2021. Rendered December 13, 2024 14:40
CET by rmarkdown via pandoc in 0.44 seconds.
Footnotes and References
Therneau TM, Lumley T, Atkinson E, Crowson C. Survival Analysis. Package version 3.7.0. 2024-06-01. CRAN↩︎
Hothorn T, Winell H, Hornik K, van de Wiel MA, Zeileis A. Conditional Inference Procedures in a Permutation Test Framework. Package version 1.4.3. 2023-09-26. CRAN↩︎
Mersman O, Trautmann H, Steuer D, Bornkamp B. truncnorm: Truncated Normal Distribution. Package version 1.0.9. 2023-03-20. CRAN.↩︎
Wickham H. Flexibly Reshape Data. Package version 0.8.9. 2022-04-12. CRAN.↩︎
Sarkar D, Andrews F, Wright K, Klepeis, N, Murrell P. Trellis Graphics for R. Package version 0.22.6. 2024-03-20. CRAN.↩︎
Komsta L, Novomestky F. moments: Moments, Cumulants, Skewness, Kurtosis and Related Tests. Package version 0.14.1. 2015-01-05. CRAN.↩︎
Commission of the European Community. Investigation of Bioavailabilty and Bioequivalence. Brussels. December 1991.
 BEBAC
Archive.↩︎
BEBAC
Archive.↩︎EMEA, CPMP. Note for Guidance on the Investigation of Bioavailability and Bioequivalence. London. 26 July 2001. Online.↩︎
EMA, CHMP. Guideline on the Investigation of Bioequivalence. London. 20 January 2010. Online.↩︎
EMA, CHMP. Guideline on the pharmacokinetic and clinical evaluation of modified release dosage forms. 20 November 2014. Online.↩︎
EMA, CHMP. Ibuprofen oral use immediate release formulations 200 – 800 mg product-specific bioequivalence guidance. Amsterdam. 26 April 2023. Online.↩︎
EMA, CHMP. Paracetamol oral use immediate release formulations product-specific bioequivalence guidance. Amsterdam. 26 April 2023. Online.↩︎
EMA, CHMP. Tadalafil film-coated tablets 2.5 mg, 5 mg, 10 mg and 20 mg product-specific bioequivalence guidance. Amsterdam. 26 April 2023. Online.↩︎
Sauter R, Steinijans VW, Diletti E, Böhm E, Schulz H-U. Presentation of results from bioequivalence studies. Int J Clin Pharm Ther Toxicol. 1992; 30(7): 233–56. PMID:1506127.↩︎
ANMAT. Régimen de Buenas Prácticas para la Realización de Estudios de Biodisponibilidad/Bioequivalencia. Buenos Aires. 2006. Online. [Spanish].↩︎
NIHS, Division of Drugs. Guideline for Bioequivalence Studies of Generic Products. Q & A. Tokio. February 29, 2012. Online.↩︎
NIHS, Division of Drugs. Guideline for Bioequivalence Studies of Generic Products. Q & A. Tokio. March 19, 2020. Online.↩︎
MCC. Registration of Medicines. Biostudies. Pretoria. June 2015. Online.↩︎
EMEA, CPMP. Note for Guidance on Modified Release Oral and Transdermal Dosage Forms: Section II (Pharmacokinetic and Clinical Evaluation). London. 28 July 1999. Online.↩︎
Department of Health, TGA. European Union and ICH Guidelines adopted in Australia. Guideline on the Investigation of Bioequivalence with TGA Annotations. Canberra. 16 June 2011. Online↩︎
ASEAN States Pharmaceutical Product Working Group. ASEAN Guideline for the Conduct of Bioequivalence Studies. Vientiane. March 2015. Online.↩︎
ANAMED. Instituto de Salud Pública de Chile. Guia para La realización de estudios de biodisponibilidad comparativa en formas farmacéuticas sólidas de administración oral y acción sistémica. Santiago. December 2018. [Spanish].↩︎
ECC. Regulations Conducting Bioequivalence Studies within the Framework of the Eurasian Economic Union. 3 November 2016, amended 4 September 2020. Online.↩︎
Ministry of Health and Population, The Specialized Scientific Committee for Evaluation of Bioavailability & Bioequivalence Studies. Egyptian Guideline For Conducting Bioequivalence Studies for Marketing Authorization of Generic Products. Cairo. February 2017.
 Internet
Archive.↩︎
Internet
Archive.↩︎Executive Board of the Health Ministers’ Council for GCC States. The GCC Guidelines for Bioequivalence. Version 3.1. 10 August 2022. Online.↩︎
New Zealand Medicines and Medical Devices Safety Authority. Guideline on the Regulation of Therapeutic Products in New Zealand. Part 6: Bioequivalence of medicines. Wellington. February 2018. Online.↩︎
WHO, Essential Medicines and Health Products: Multisource (generic) pharmaceutical products: guidelines on registration requirements to establish interchangeability. WHO Technical Report Series, No. 1003, Annex 6. Geneva. 28 April 2017. Online↩︎
The true tmax follows a continuous distribution. However, due to the sampling schedule the distribution is discretized.↩︎
Think about normal distributed data. The arithmetic mean is the statistic of location (central tendency) and the standard deviation the statistic of dispersion. Both are estimated values. Talking about the ‘variability’ of the mean would be nonsense as well.↩︎
Johnston RG, Schroder SA, Mallawaaratchy AR. Statistical Artifacts in the Ratio of Discrete Quantities. Am Stat. 1995; 49(3): 285–91. JSTOR:2684202.↩︎
Basson RP, Cerimele BJ, DeSante KA, Howey DJ. Tmax: An Unconfounded Metric for Rate of Absorption in Single Dose Bioequivalence Studies. Pharm Res. 1996; 13(2): 324–8. doi:10.1023/A:1016019904520.↩︎
Tóthfálusi L, Endrényi L. Estimation of Cmax and Tmax in Populations After Single and Multiple Drug Administration. J Pharmacokin Pharmacodyn. 2003; 30(5): 363–85. doi:10.1023/b:jopa.0000008159.97748.09.↩︎
Endrényi L, Tóthfalusi L. Metrics for the Evaluation of Bioequivalence of Modified-Release Formulations. AAPS J. 2012; 14(4): 813–9. doi:10.1208/s12248-012-9396-8.
 Free
Full Text.↩︎
Free
Full Text.↩︎Geyer CJ. Nonparametric Tests and Confidence Intervals. April 13, 2003. Online.↩︎
Imagine:
\(\small{x=\left\{1,\cdots,1,2\right\}\rightarrow \tilde{x}={\color{Blue}1}\;\wedge_{}^{}\;R(x)={\color{Blue}1}}\)
\(\small{y=\left\{1,\cdots,1,3\right\}\rightarrow \tilde{x}={\color{Blue}1}\;\wedge_{}^{}\;R(y)={\color{Red}2}}\)
Is the range of \(\small{y}\) ‘apparently’ different from the one of \(\small{x}\)?
\(\small{z=\left\{1,\cdots,1,1\right\}\rightarrow \tilde{x}={\color{Blue}1}\;\wedge_{}^{}\;R(z)={\color{Red}0}}\)
Is the range of \(\small{z}\) ‘apparently’ different from the other ones?↩︎Note that the function
wilcox.test()of Base R is not exact for tied (equally ranked) data. Hence, I used the functionwilcox_test()of packagecoinwith its default average ranking.↩︎Wagener HH, Vögtle-Junkert U. Intrasubject variability in bioequivalence studies illustrated by the example of ibuprofen. Int J Clin Pharmacol Ther. 1996; 34(1): 21–31. PMID:8688993.↩︎
In models with more than one compartment \(\small{t_\text{max}}\) and \(\small{C_\text{max}}\) cannot be analytically derived. In software numeric optimization is employed to locate the maximum of the function.↩︎
That explains why PD is less sensitive to detect differences in formulations and PK-studies are preferred.↩︎
Basson RP, Ghosh A, Cerimele BJ, DeSante KA, Howey DC. Why Rate of Absorption Inferences in Single Dose Bioequivalence Studies are Often Inappropriate. Pharm Res. 1998; 15(2): 276–9. doi:10.1023/a:1011974803996.↩︎
Hauschke D, Steinijans VW, Diletti E. A distribution-free procedure for the statistical analysis of bioequivalence studies. Int J Clin Pharm Ther Toxicol. 1990; 28(2): 72–8. PMID:2307548.↩︎
Brunner E, Munzel U. The Nonparametric Behrens‐Fisher Problem: Asymptotic Theory and a Small‐Sample Approximation. Biom. J. 2000; 42(1): 17–25. doi:10.1002/(SICI)1521-4036(200001)42:1%3C17::AID-BIMJ17%3E3.0.CO;2-U.↩︎
Neubert K, Brunner E. A studentized permutation test for the non-parametric Behrens–Fisher problem. Comput Stat Data Anal. 2007; 51(10): 5192–204. doi:10.1016/j.csda.2006.05.024.↩︎
Wilcox RA. Introduction to Robust Estimation and Hypothesis Testing. London: Academic Press; 4th ed. 2017. p. 192–8.↩︎
Chow S-C, Liu J-p. Design and Analysis of Bioavailability and Bioequivalence Studies. Boca Raton: Chapman & Hall / CRC; 3rd ed. 2009. Table 5.3.4. p. 146.↩︎
FDA, CDER. Draft Guidance for Industry. Bioequivalence Studies with Pharmacokinetic Endpoints for Drugs Submitted Under an ANDA. Rockville. December 2013. Download↩︎
Health Canada. Guidance Document. Comparative Bioavailability Standards: Formulations Used for Systemic Effects. Ottawa. 2018/06/08. Online↩︎
Will that inflate the Type I Error because it depends on the observed data? Perhaps. However, since only the point estimate is assessed, likely the overall Type I Error is controlled by the 90% CI of AUC.↩︎
FDA, CDER. Guidance for Industry. Bioavailability and Bioequivalence Studies for Orally Administered Drug Products — General Considerations. Rockville. March 2003.
 Internet
Archive.↩︎
Internet
Archive.↩︎FDA, CDER. Guidance for Industry. Bioavailability Studies Submitted in NDAs or INDs — General Considerations. Silver Spring. April 2022. Download.↩︎
FDA, OGD. Draft Guidance on Methylphenidate Hydrochloride. Recommended Sept 2012; Revised Nov 2014; Jul 2018. Download.↩︎
ICH. Bioequivalence for Immediate-Release Solid Oral Dosage Forms. M13A. Geneva. 23 July 2024. Online .↩︎
Bonate PL. Pharmacokinetic-Pharmacodynamic Modeling and Simulation. New York: Springer; 2nd ed. 2011. p. 359.↩︎
Gabrielsson J, Weiner D. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications. Stockholm: Apotekarsocieteten; 5th ed. 2016. p. 335–6, p. 704.↩︎
Kant I. Answering the Question: What Is Enlightenment? Berlinische Monatsschrift. December 1784. [Original in German].↩︎

